
题目列表(包括答案和解析)
27、(本小题满分12分)
解: (I)设点A(x1,0),B(x2,0) .
则x1 ,x2是方程 x2-mx+m-2=0的两根. ………1分
∵x1 + x2 =m , x1·x2 =m-2 <0 即m<2 ; ………2分
又AB=∣x1 - x2∣=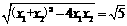 ,
………3分
,
………3分
∴m2-4m+3=0 . ………4分
解得:m=1或m=3(舍去) , ………5分
∴m的值为1 . ………6分
(II)设M(a,b),则N(-a,-b) .
∵M、N是抛物线上的两点,
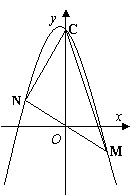 ∴
∴ ………7分
………7分
①+②得:-2a2-2m+4=0 .
∴a2=-m+2 . ………8分
∴当m<2时,才存在满足条件中的两点M、N.
∴ .
………9分
.
………9分
这时M、N到y轴的距离均为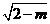 ,
………10分
,
………10分
又点C坐标为(0,2-m),而S△M N C = 27 ,
∴2×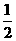 ×(2-m)×
×(2-m)×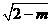 =27 .
…… 11分
=27 .
…… 11分
∴解得m=-7 . ………12分
26、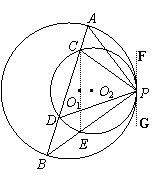 (本小题满分12分)
(本小题满分12分)
(I)证法一:
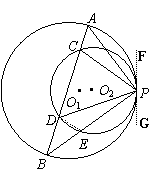
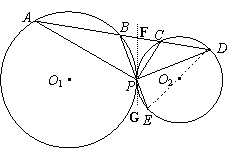
过点P作⊙O1、⊙O2的公切线FG,
连结CE. ………1分
在⊙O1 中,∠GPB=∠A , ………2分
在⊙O2中,∠GPB=∠ECP , ………3分
∴∠A=∠ECP . ………4分
又∵∠ADP=∠CEP,
∴△ADP∽△CEP . ………5分
∴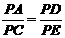 .
.
即PA·PE=PD·PC . ………6分
证法二:
过点P作⊙O1、⊙O2的公切线FG,
连结DE. ………1分
在⊙O1 中,∠GPB=∠A , ………2分
 在⊙O2中,∠GPB=∠EDP ,
………3分
在⊙O2中,∠GPB=∠EDP ,
………3分
又∵四边形CDEP为⊙O2 的内接四边形,
∴∠ACP=∠DEP . ………4分
∴△ACP∽△DEP . ………5分
∴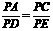 .
.
即PA·PE=PD·PC . ………6分
(II)结论仍然成立. ………7分
证法一:
过点P作⊙O1、⊙O2的内公切线FG,
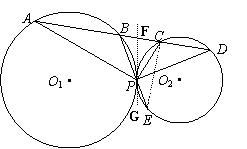 连结CE.
………8分
连结CE.
………8分
在⊙O1 中,∠FPB=∠A ,
在⊙O2中,∠GPE=∠PCE ,
而∠GPE=∠FPB ,
∴∠A=∠PCE . ………10分
又∵∠ADP=∠CEP ,
∴△ADP∽△CEP . ………11分
∴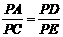 .
.
即PA·PE=PD·PC . ………12分
证法二:
 过点P作⊙O1、⊙O2的内公切线FG,
过点P作⊙O1、⊙O2的内公切线FG,
连结DE. ………8分
在⊙O1 中,∠FPB=∠A ,
在⊙O2中,∠GPE=∠PDE ,
而∠GPE=∠FPB ,
∴∠A=∠PDE . ………10分
又∵∠ACP=∠DEP ,
∴△ACP∽△DEP . ………11分
∴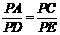 .
.
即PA·PE=PD·PC . ………12分
25、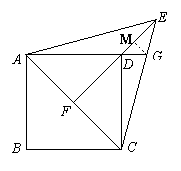 (本小题满分10分)
(本小题满分10分)
(I)证明:由已知,得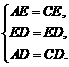
∴△AED≌△CED . ………2分
∴∠AED=∠CED . ………3分
又∵△AEC为等边三角形,
∴EF⊥AC . ………4分
(II)解法一:
过G作GM⊥EF,垂足为M. ………5分
由已知和(Ⅰ) ,得
∠AED=∠CED=30o,∠EAD=150 .
∴∠EDG=45o .
∴MD=GM . ………6分
设GM=x,则DG=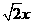 .
.
在Rt△MEG中,EG=2MG=2x , ………7分
∴EM=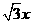 .
………8分
.
………8分
∴ED=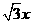 +
+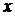 =(
=(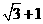 )
)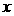 .
………9分
.
………9分
∴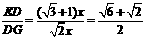 .
.
即DE=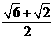 DG ( 或
DG ( 或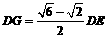 ) .
……10分
) .
……10分
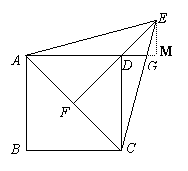 解法二:
解法二:
过E作EM⊥AD,垂足为M. ………5分
在Rt△MDE中,
∵∠EDM=∠MED =45o ,
∴EM=DM .
设EM=DM=x,
则DE=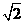 x .
………6分
x .
………6分
在Rt△AEF中,cot300=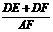 ,
,
∴DF=AF=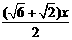 .
………7分
.
………7分
∴AD=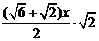 .
.
=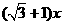 .
………8分
.
………8分
∵△CDG∽△AME ,
∴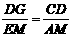 .
.
即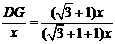 .
.
∴DG=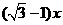 .
………9分
.
………9分
∴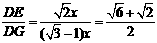 .
.
即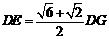 ( 或
( 或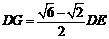 ). ………10分
). ………10分
24、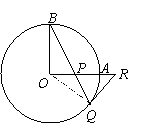 (本小题满分10分)
(本小题满分10分)
(I)证法一:
连结OQ . ………1分
∵RQ是⊙O的切线,
∴∠OQB+∠BQR=90O . ………2分
∵OA⊥OB,
∴∠OPB+∠B =90O . ………3分
又∵OB=OQ,
∴∠OQB=∠B .
∴∠PQR=∠BPO=∠RPQ . ………4分
∴RP=RQ . ………5分
证法二:
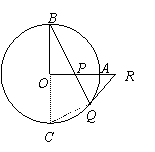 作直径BC,连结CQ . ………1分
作直径BC,连结CQ . ………1分
∵BC是⊙O的直径,
∴∠B+∠C=90O . ………2分
∵OA⊥OB,
∴∠B+∠BPO=90O .
∴∠C=∠BPO . ………3分
又∠BPO=∠RPQ,
∴∠C=∠RPQ.
又 ∵RQ为⊙O的切线,
 ∴∠PQR=∠C .
………4分
∴∠PQR=∠C .
………4分
∴∠PQR=∠RPQ.
∴RP=RQ . ………5分
(II)解法一:
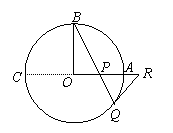
作直径AC. ………6分
∵OP=PA=1,
∴PC=3 . ………7分
由勾股定理,得BP=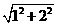 =
=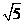 . ………8分
. ………8分
由相交弦定理,得PQ·PB=PA·PC . ………9分
即PQ×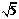 =1×3.
=1×3.
∴PQ=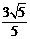 .
………10分
.
………10分
解法二:
作直径AE,
过R作RF⊥BQ ,垂足为F . ………6分
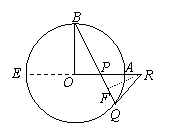 设RQ=RP=x,
设RQ=RP=x,
由切割线定理,得:x2=(x-1)(x+3).
解得:x=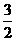 .
………7分
.
………7分
又由△BPO∽△RPF得 :
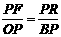 ,
………8分
,
………8分
∴PF=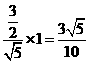 .
………9分
.
………9分
由等腰三角形性质得:PQ=2PF=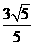 .………10分
.………10分
23、(本小题满分8分)
解:(I)
|
年份 |
2000年 |
2001年 |
2002年 |
|
工人的平均工资 |
5000 |
6250 |
7500 |
|
股东的平均利润 |
25000 |
37500 |
50000 |
………4分(说明:每空1分)
(II)设经过x年每位股东年平均利润是每位工人年平均工资的8倍.
由图可知:
每位工人年平均工资增长1250元,
每位股东年平均利润增长12500元 , ………5分
所以 (5000+1250x)×8=25000+12500x. ………6分
解得 x=6 . ………7分
答:到2006年每位股东年平均利润是每位工人年平均工资的8倍. ………8分
22、(本小题满分8分)
解法一:设 ,
………1分
,
………1分
则原方程可化为: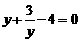 .
………2分
.
………2分
去分母,并整理得:y2-4y+3=0 . ………3分
解得:y1=1, y2=3 . ………4分
当y1=1时, ,解得
,解得 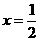 ;
;
当y2=3时, 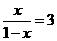 ,解得
,解得 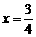 .
………6分
.
………6分
经检验,x1=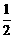 ,x2=
,x2=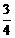 都是原方程的根. ………8分
都是原方程的根. ………8分
解法二:
去分母,得:x2+3(1-x)2-4x (1-x)=0 . ………2分
化简,得:8x2-10x+3=0 . ………4分
解得:x1=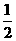 ,x2=
,x2= .
………6分
.
………6分
经检验,x1=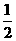 ,x2=
,x2= 都是原方程的根. ………8分
都是原方程的根. ………8分
21、(本小题满分6分)
解法一:
由已知,得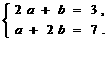 ………2分
………2分
两式相加,得:3a+3b=10 . ………5分
∴a+b=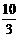 .
………6分
.
………6分
解法二:
由已知,得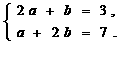 ………2分
………2分
解得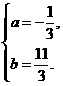 ………5分
………5分
∴ .
………6分
.
………6分
20、(本小题满分6分)
解法一:
原式=(a3+a2b)-(ab2+b3) ………1分
=a2(a+b)-b2(a+b) ………2分
=(a+b)(a2-b2) ………4分
=(a+b) (a+b) (a-b) ………5分
=(a+b)2(a-b) ………6分
解法二:
原式=(a3-ab2)+(a2b-b3) ………1分
=a(a2-b2)+b(a2-b2) ………2分
=(a2-b2)(a+b) ………4分
=(a+b)(a-b)(a+b) ………5分
=(a-b)(a+b)2. ………6分
19、(本小题满分6分)
解:原式=6×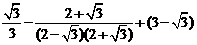 ………3分
………3分
=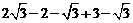 ………5分
………5分
=1 ………6分
15、0 16、小于(填“< ”给满分 ) 17、 8 18、1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com