23、 (本题满分10分)本题共有2个小题，第1小题满分6分，第2小题满分4分。

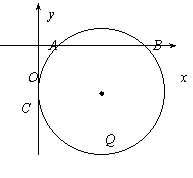圆Q交x轴于原点右侧的A、B两点，并切y轴于原点下方的C点，如图所示。已知│AB│=3，│AC│=。

(1)求A、B、C三点的坐标；

(2)如果抛物线经过A、B、C三点，求这条抛物线的解析式。

解：(1)设A(x，0)、B(x+3，0)、C(0，y)，

根据切割线定理，

。

解得：x=1或x=(舍)。∴y=-2。

∴A、B、C三点的坐标分别是A(1，0)、B(4，0)、C(0，-2)。

(2)设过两点的抛物线为y=a(x-1)(x-4)，

∵它过点C(0，-2)，∴-2=a(0-1)(0-4)，∴a==。

∴抛物线的方程为y=(x-1)(x-4)。▋

22、 对任意两个正整数x、y，定义一个运算“★”为x★y=2(x+2xy+y)，若正整数a、b满足a★b=1154，则有序正整数对(a，b)共有___14___对。

21、 在数A的右端再加上一个数字6，则该数比原数增加2004，那么A=_222___。

20、 王师傅围一块一面靠墙长方形花圃，面积为50m²，如果不靠墙的三面用竹篱笆去围。那么，竹篱笆最少需要____20_____m长。

19、 已知方程(x-19)(x-90)=p有实根r₁，r₂，其中p为实数，则方程(x-r₁)(x-r₂)=-p的最小实根是___19___。

18、 在半径为5的单位圆中，直径AB与CD互相垂直，弦CH交AB于K，且CH=8，则│AK-BK│=___7.5________。

17、 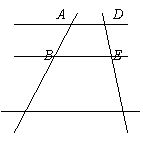如图，AD∥BE∥CF，AB=AD=1，BE=2，CF=4，则BC=___2____。

16、 设∠xOy=30°，A是射线Ox上一点，OA=2，D为射线Oy上一点，OD=3，C是射线Ox上任意一点，B是射线Oy上任意一点，则折线ABCD的长AB+BC+CD的最小值是_________。

15、 已知θ为锐角，且关于x的方程x²+3x+2sinθ=0的两根之差为，则θ=___30°____。

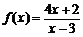14、 已知函数(c≠0)的对称中心为(a，b)，试回答：的对称中心为______(3，4)_________________。