
题目列表(包括答案和解析)
(1)求点B的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,
使得 ?若存在,请求出该点坐标,
?若存在,请求出该点坐标,
若不存在,请说明理由.
|
2004年大连市2、在平面直角坐标系中,点(-1,-2)所在的象限是 ( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限

6、如图2,直线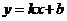 与
与 轴交于点(-4 , 0),则
轴交于点(-4 , 0),则 > 0时,
> 0时,
 的取值范围是
(
)
的取值范围是
(
)
A、 >-4 B、
>-4 B、 >0
C、
>0
C、 <-4
D、
<-4
D、 <0
<0
20.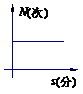
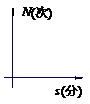
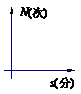
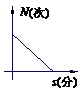 一个正常人在做激烈运动时,心跳速度加快,当运动停止下来后,心跳次数N (次)与时间s(分)的函数关系图像大致是 ( )
一个正常人在做激烈运动时,心跳速度加快,当运动停止下来后,心跳次数N (次)与时间s(分)的函数关系图像大致是 ( )
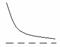

A B C D
12. 函数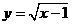 中,自变量x的取值范围是
(
)
中,自变量x的取值范围是
(
)
A. x < 1 B. x ≤ 1 C. x > 1 D. x ≥1
25.已知:在平面直角坐标系xOy中,过点P(0,2)任作一条与抛物线y=ax2(a>0)交于两点的直线,设交点分别为A、B.若∠AOB=90°,
⑴ 判断A、B两点纵坐标的乘积是否为一个确定的值,并说明理由;
⑵ 确定抛物线y=ax2(a>0)的解析式;
⑶ 当ΔAOB的面积为4时,求直线AB的解析式.
郴州市2004年
2.如图7-123,已知CB、CD切⊙O于B、D点,过B作直径交⊙O于E交CD的延长线于A,若AD=m·AE,且tg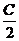 =
= ,求m的值.
,求m的值.
(1)如图7-120,BC是⊙O的直径,AB是⊙O的切线,B是切点,AB=BC,AC交⊙O于
D,E在CB的延长线上,BE=BC,DE交⊙O于F,求证AF⊥DE.

(2)如图7-121,M为弦AB的中点,C为圆上任意一点,切线AD交CB的延长线于D,连DM并延长交AC于E,求证AD2:BD2=CE:AE.

[素质优化训练]
1.如图7-122,AB是⊙O的直径,CD⊥AB于D,CT切⊙O于T,求证:BE2+CT2=BC2.

(1)圆的两弦相交,一弦被分为12cm和8cm两段,另一弦被分为3:8,则另一弦长是( )
A.11cm B.9 cm C.22cm D.33cm
(2)圆内接正方形ABCD的边长为2,弦AK平分边BC,则AK的长为( )
A.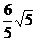 B.
B.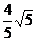 C.
C. D.
D.
(3)从圆外一点向半径为9的圆作切线,已知切线长为18,则从这一点到圆的最短距离是( )
A.9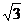 B.9
B.9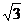 -9 C.9
-9 C.9 -9
D.9
-9
D.9
(4)已知⊙O外一定点P,P与O的距离为4cm,从P点向圆作切线,切线长与圆的半径之差为2cm,则圆的半径为( )
A.(1+ )cm
B.(
)cm
B.( -1)cm或(1+
-1)cm或(1+ )cm
)cm
C.( -1)cm或(1+
-1)cm或(1+ )cm
D.(
)cm
D.( -1)cm
-1)cm
(5)已知PA是圆的切线,A为切点,PBC是圆的割线,与圆相交于B、C两点,若PB=3,BC=6,则PA的长为( )
A.6
B.2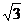 C.3
C.3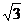 D.3
D.3
(1)⊙O内弦CD垂直于直径AB,E为垂足,且AE=4cm,BE=9cm,CD=_4 _.
_.
(2)圆内两相交弦,一弦长3cm被交点平分,另一弦被交点分成1:4,则此弦长为______.
(3)已知圆的切线PT的长是6cm,割线PAB的长是9cm,则弦AB的长是______.
(4)在直径为2的圆外有一点P到圆的最近点的距离为3,则过这点的切线长是______.
(5)⊙O的割线PAB交⊙O于A、B两点,已知:PA=6cm,AB=7 cm,PO=12cm,则⊙O的半径为______.
cm,PO=12cm,则⊙O的半径为______.
5. (安徽03/21)如图是五角星,已知AC=a,求五角星外接圆的直径(结果用含三角函数的式子表示)。

[解]

4.
2003资阳市如图,在△ABC中,已知∠ACB=90°,CD⊥AB于D,AC= ,BD=3。
,BD=3。
(1)请根据下面求cosA的解答过程,在横线上填上适当的结论,使解答正确完整:
∵CD⊥AB ∠ACB=90°
∴AC= AB cosA, AD =AC·cosA
由已知AC= ,BD=3
,BD=3
∴ =AB cosA=(AD+BD)cosA=(
=AB cosA=(AD+BD)cosA=( cosA+3)cosA
cosA+3)cosA
设 =cosA,则
=cosA,则 >0,且上式可化为
>0,且上式可化为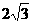
 +
+ -
-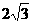 =0,则此解得cosA=
=0,则此解得cosA= =
=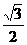
(2)求BC的长及△ABC的面积。

(2)解:在Rt△ABC中,BC=AC·tanA= ·
·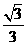 =6
=6
S△ABC=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com