
题目列表(包括答案和解析)
3.下列各式中去括号正确的是( )
A.  B.
B. 
C.  D.
D. 
2.下列说法正确的是( )
A. 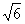 是根式也是整式 B.实数a的相反数是-a是负数
是根式也是整式 B.实数a的相反数是-a是负数
C.实数a的倒数是  D.带根号的数是无理数
D.带根号的数是无理数
1.下列式子中,正确的是( )
A. 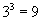 B.
B.  C.
C.  D.
D. 
(19)(本小题6分)
在一次数学知识竞赛中,某班20名学生的成绩入下表所示:
|
成 绩 (单位:分) |
50 |
60 |
70 |
80 |
90 |
|
人 数 |
2 |
3 |
6 |
7 |
2 |
分别求这些学生成绩的众数、中位数、和平均数.
(20)(本小题8分)
解方程
 .
.
(21)(本小题8分)
已知抛物线y=x2+bx+c与x轴只有一个交点,且交点为A(2,0).
(Ⅰ)求b、c的值;
(Ⅱ)若抛物线与y轴的交点为B,坐标原点为O,求△OAB的周长
(答案可带根号).
(22)(.本小题8分)
已知一次函数y=x+m与反比例函数y=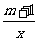 (x≠-1)的图象在第一象限内的交点为P(x0,3).
(x≠-1)的图象在第一象限内的交点为P(x0,3).
(Ⅰ)求x0的值;
(Ⅱ)求一次函数和反比例函数的解析式.
(23)(.本小题8分)
如图,已知PAB是⊙O的割线,AB为⊙O的直径,PC为⊙O的切线,C为切点,BD⊥PC于点D,交⊙O于点E,PA=AO=OB=1.
 (Ⅰ)求∠P的度数;
(Ⅰ)求∠P的度数;
(Ⅱ)求DE的长.
(24)(本小题8分)
在建筑楼梯时,设计者要考虑楼梯的安全程度,如图1,虚线为楼梯的斜度线,
斜度线与地板的夹角为倾角θ,一般情况下, 倾角θ 愈小,楼梯的安全程度愈高.
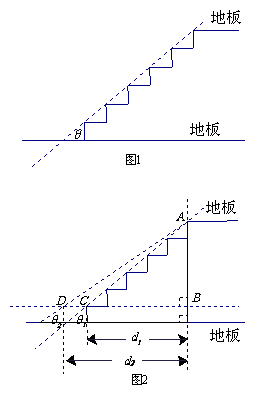 如图2,设计者为提高楼梯的安全程度,要把楼梯的倾角由θ1减至θ2,这样楼梯占用地板的长度由d1增加到d2,已知d1=4m,∠θ1=40°,∠θ2=36°,求楼梯占用地板的长度增加了多少?(精确到0.01m)
如图2,设计者为提高楼梯的安全程度,要把楼梯的倾角由θ1减至θ2,这样楼梯占用地板的长度由d1增加到d2,已知d1=4m,∠θ1=40°,∠θ2=36°,求楼梯占用地板的长度增加了多少?(精确到0.01m)
参考数据:
sin36°=0.5878 cos36°=0.8090
tan36°=0.7265 sin40°=0.6428
cos40°=0.7660 tan40°=0.8391
(25)(本小题10分)
已知A为⊙O上一点,B为⊙A与OA的交点,⊙A与⊙O的半径分别为r、R,且r<R.
(Ⅰ)如图,过点B作⊙A的切线与⊙O交于M、N两点.
 求证:AM·AN=2Rr;
求证:AM·AN=2Rr;
 (Ⅱ)如图,若⊙A与⊙O的交点为E、F,C是弧EBF上任意一点,过点C作⊙A的切线与⊙O交于P、Q两点,试问AP·AQ=2Rr是否成立,并证明你的结论.
(Ⅱ)如图,若⊙A与⊙O的交点为E、F,C是弧EBF上任意一点,过点C作⊙A的切线与⊙O交于P、Q两点,试问AP·AQ=2Rr是否成立,并证明你的结论.
(26) (本小题10分)
已知一次函数y1=2x,二次函数y2=x2+1.
(Ⅰ)根据表中给出的x的值,计算对应的函数值y1、y2,并填在表格中:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y1=2x |
|
|
|
|
|
|
|
|
y2=x2+1 |
|
|
|
|
|
|
|
(Ⅱ)观察第(Ⅰ)问表中有关的数据,证明如下结论:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1≤y2均成立;
(Ⅲ)试问,是否存在二次函数y3=ax2+bx+c,其图象经过点(-5,2),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≤y3≤y2均成立,若存在,求出函数y3的解析式;若不存在,请说明理由.
答案直接填在题中横线上.
(11)不等式 5x -9≤3(x+1)的解集是 .
(12)已知关x的方程x2-3x+m=0的一个根是另一个根的2倍,则m的值为________.
(13) 已知⊙O1和⊙O2相外切,且圆心距为10cm,若⊙O1半径为3cm,则⊙O2的半径为__________cm.
 (14) 如图,等腰梯形ABCD中,对角线AC、BD相交于点O,
(14) 如图,等腰梯形ABCD中,对角线AC、BD相交于点O,
那么图中的全等三角形最多有________对. (第(14)题图)
(15) 已知x2+y2=25,x+y=7,且x>y,则x-y的值等于___________.
(16) 若a、b都是无理数,且a+b=2,则a、b的值可以是______________________.
(填上一组满足条件的值即可)

(17) 如图,已知两个等圆⊙O1与⊙O2相交于A、B两点,一条直线经过点A,分别与两圆相交于点C、D,MC切⊙O1于点C,MD切⊙O2于点D,若∠BCD=30°,则∠M等于________(度)
(18)已知正方形ABCD的边长是1,E为CD边的中点,
P为正方形ABCD边上的一个动点,动点P从A点


 出发,沿A B C E运动,到达点E.
出发,沿A B C E运动,到达点E.
若点P经过的路程为自变量x,△APE的面积为函数y,则当
y= 时,x的值等于___________________.
时,x的值等于___________________.
2.第Ⅱ卷共8页,用蓝、黑色墨水的钢笔或圆珠笔直接答在试卷上.
(1) 2Sin450的值等于
(A) 1 (B)
(C)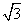 (D)
2
(D)
2
(2) 若x<2,则  的值为
的值为
(A)-1 (B) 0
(C) 1 (D) 2
(3) 在下列图形中,即是轴对称图形,又是中心对称图形的是

(A) (B) (C) (D)
(4) 若一个正多边形的每一个内角都等于120°,则它是
(A) 正方形 (B) 正五边形
(C) 正六边形 (D)正八边形
(5) 下列命题中正确的是
(A)对角线互相平分的四边形是菱形
(B) 对角线互相平分且相等的四边形是菱形
(C) 对角线互相垂直的四边形是菱形
(D) 对角线互相垂直平分的四边形是菱形

 (6) 如图,⊙O的两条弦AB、CD相交于点E,AC与DB的延长线交于点P,
(6) 如图,⊙O的两条弦AB、CD相交于点E,AC与DB的延长线交于点P,
下列结论中成立的是
(A)CE·CD=BE·BA
(B)CE·AE=BE·DE
(C)PC·CA=PB·BD
(D)PC·PA=PB·PD (第(6)题图)
(7) 为适应国民经济持续协调的发展,自2004年4月18日起,全国铁路第五次提速,提速后,火车由天津到上海的时间缩短了7.42小时,若天津到上海的路程为1326千米,提速前火车的平均速度为x千米/小时,提速后火车的平均速度为y千米/时,则x、y应满足的关系式是
(A)x – y
=  (B)
y – x =
(B)
y – x = 
(C)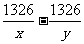 = 7.42
(D)
= 7.42
(D) 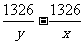 = 7.42
= 7.42
(8) 已知二次函数 y=ax2+bx+c,且a<0,a-b+c>0,则一定有
(A)b2-4ac>0 (B) b2-4ac=0
(C) b2-4ac<0 (D) b2-4ac≤0
(9) 如图,已知等腰 中,顶角∠A=36°,BD为∠ABC的平分线,
中,顶角∠A=36°,BD为∠ABC的平分线,
 则
则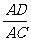 的值等于
的值等于
(A) (B)
(B)
(C) 1
(D) (第(9)题图)
(第(9)题图)
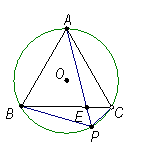 (10) 如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:① PA=PB+PC, ②
(10) 如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:① PA=PB+PC, ②  ;③ PA·PE=PB·PC.其中,正确结论的个数为
;③ PA·PE=PB·PC.其中,正确结论的个数为
(A) 3个 (B) 2个
(C) 1个 (D) 0个
(第(10)题图
第Ⅱ卷 (非选择题 共90分)
1.答第Ⅱ卷时,考生务必将密封线内的项目和试卷第三页右上角
的“座位号”填写清楚.
26、已知:抛物线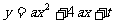 与
与 轴的一个交点为A(-1,0)。
轴的一个交点为A(-1,0)。
(1)求抛物线与 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
(2)D是抛物线与 轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;
轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;
(3)E是第二象限内到 轴、
轴、 轴的距离的比为5∶2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧。问:在抛物线的对称轴上,是否存在点P,使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由。
轴的距离的比为5∶2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧。问:在抛物线的对称轴上,是否存在点P,使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由。
25、已知,在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,FE∶FD=4∶3。
(1)求证:AF=DF;
(2)求∠AED的余弦值;
(3)如果BD=10,求△ABC的面积。

24、已知关于 的方程
的方程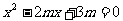 的两个实数根为
的两个实数根为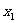 、
、 ,且
,且 如果关于
如果关于 的另一方程
的另一方程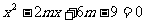 的两个实数根都在
的两个实数根都在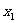 和
和 之间,求
之间,求 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com