6．(2002　 北京海淀区)已知：关于x的方程(n–1)x²+mx+1=0　 ①　　 有两个相等的实数根。 　⑴求证：关于y的方程m²y²–2my–m²–2n²+3=0　 ②　　 必有两个不相等的实数根； 　⑵若方程①的一根的相反数恰好是方程②的一个根，求代数式m²n+12n的值。

5.(北京东城区)已知关于x的方程x²-(k-1)x+k+1=0的两个实数根的平方和等于4，求实数k的值。

4．(北京西城区)解方程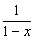：-2=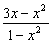

3．( 荆门市)已知关于x的方程x²–(k+2)x+2k=0 　(1)求证无论K取任何实数值，方程总有实数根。 　(2)若等腰三角形的一边长为a=1，另两边恰是这个方程的两个根，求△ABC的周长。

2．(2002　 北京崇文区)求不等式组的整数解。

3.(2002　 北京西城区)如果关于x的方程2x²–7x+m=0的两个实数根互为倒数，那么m的值为(　 ) 　A、　B、-　C、2　D、-2

2．(2002　 北京东城区)关于x的一元二次方程(a–1)x²+x+a²–1=0的一个根是0，则a的值为(　 ) 　A、1　B、-1　C、1或-1　D、

7.(北京东城区)商场出售的A型冰箱每台售价2190元，每日耗电量为1度，而B型节能冰箱每台售价虽比A型冰箱高出10%，但每日耗电量却为0.55度。现将A型冰箱打折出售(打一折后的售价为原价的)，问商场至少打几折，消费者购买才合算(按使用期为10年，每年365天，每度电0.40元计算)？

　考点：一元一次不等式的应用

　评析：列一元一次不等式解应用题首先要弄清题意设出适当的未知数。消费者要买A型冰箱，10年的花费用比B型少才行，设打x折，那么A型10年的费用为2190×+365×10×1×0.40，B型10年的费用为2190×(1+10%)+365×10×0.55×0.40，根据题意得不等式2190×+365×10×1×0.40≤2190×(1+10%)+365×10×0.55×0.40，解得x8，所以至少打八折，解题过程如下：

　解：设商场将A型冰箱打x折出售，消费者购买才合算

　依题意，有 　2190×+365×10×1×0.4≤2190×(1+10%)+365×10×0.55×0.4

　即 219x+1460≤2409+803

　解这个不等式，得 x≤8

　答：商场应将A型冰箱至少打八折出售，消费者购买才合算。

6.(河南省)已知一直角三角形的三边为a、b、c，∠B=90°，那么关于x的方程a(x²-1)-2cx+b(x²+1)=0的根的情况为(　 ) 　A、有两个相等的实数根　B、有两个不相等的实数根　C、没有实数根　D、无法确定

　考点：勾股定理、根的判别式

　评析：该题是一道几何代数综合型试题，因为三角形是直角三角形，∠B＝90°，根据勾股定理则有b²=a²+c²，将方程a(x²-1)-2cx+b(x²+1)=0化为一般形式为 　(a+b)x²-2cx+(b-a)=0。那么△=(-2c)²-4(a+b)·(b-a)=4c²-4b²+4a²=4[(a²+c²)-b²]，又b²=a²+c²，所以△=0，原方程有两个相等实数根，故选A。

5.(河北省)在一次“人与自然”知识竞赛中,竞赛试题共有25道题,每道题都给出4个答案,其中只有一个答案正确,要求学生把正确答案选出来,每道题选对得4分,不选或选错倒扣2分。如果一个学生在本次竞赛中的得分不低于60分,那么,他至少选对了________________道题。

　考点：一元一次不等式的应用

　评析：可设选对了x道，那么选错或不选的共有(25–x)道题。根据题意，可以列不等式为4x–2(25–x)≥60，解不等式得x≥18，取解集中的最小整数为19。

　说明：列不等式解的应用题：一般所求问题有至少、或最多、或不低于等词的要求，要正确理解这几个词的含义。