6．在ΘO中，AB是直径，弦BC等于半径，则∠ABC=　　　 。

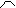　 　 7．已知　 P为半径是5cm的ΘO内一点，PO=3cm，则过P的最长的弦长为　　　 cm，最短的弦长为　　　 cm。

5．在Rt△ABC中，∠C=90°，如果sin(90°－A)=，那么cot(90°－A)=　　　 ，tanB=

　　　　 .

4．一气球在离地面55米的上空，此时一观测器测得它的仰角为30°，则观测器与气球间的距离是　　　　 。

3．已知α、β、γ都是锐角，且sinα=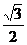，tanβ=，cotγ=1,则=　　　

2．若α、β为锐解，且tanα=cotβ，则α+β=　　　 。

1．已知∠A+∠B=90°，sinA=，则cosB=　　　　 。

28、为了测量校园内办公楼前一棵不可攀的树的高度，初三·六班数学兴趣小组做了如下的探索：

实践一：根据《物理》教科书中光的反射定律，利用一面镜子和一根皮尺，设计如图1的测量方案：把镜子放在离树8.7米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里能看到树梢顶点A，再用皮尺量得DE＝2.9米，观测者身高CD＝1.6米，请你计算树AB的高度(精确到0.1米)

实践二：提供选用的测量工具有：①皮尺一根；② 教学用三角板一副； ③高度为1.5米的测角仪(能测量仰角和俯角的仪器)一架，请用你所学的解直角三角形的有关知识，设计出求树高的方案，根据你所设计的测量方案，回答下面问题：

(1)在你设计的方案中，选用的测量工具是(填序号)　　　　　　　 ；

(2)在图2中画出你的设计方案和测量示意图；

(3)你需要测量的数据和角度分别用、、、、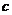、、表示；

(4)写出求树高的表达式：AB＝　　　　　　　　　　　　　　　　　 。

27、今年入夏以来，松花江哈尔滨段水位不断下降，达到历史最低水位。一条船在松花江某水段自西向东沿直线航行，如图，在A处测得航标C在北偏东60⁰方向上。前进100米到达B处，又测得航标C在北偏东45⁰方向上。在以航标C为圆心，120米长为半径的圆形区域内有浅滩。如果这条船继续前进，是否有被浅滩阻碍的危险？(供考生参考的数据：≈1.732)

26、已知△ABC中，∠A、∠B、∠C的对边分别是、、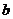 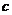(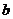＞)，关于的方程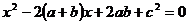有两个相等的实数根。若∠A、∠B的余弦是关于的方程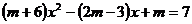的两个根。且△ABC的周长为24。

(1)试判定△ABC的形状，并证明你的结论；

(2)试求△ABC最大边的长度。

25、已知，如图：正方形ABCD中，E、F是AD上的两点，EF＝3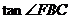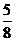，＝，＝，求FD的长。