

题目列表(包括答案和解析)
8、下列用英文字母设计的五个图案中既是轴对称图形,又是中心对称图形的有( )
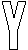
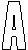

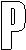
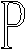

(A) 0个 (B) 1个 (C) 2个 (D)3个
7、下列三个命题:①同们角相等,两直线平行;②两点之间,线段最短;③过两点有且只有一条直线,其中真命题有( )
(A)0个 (B)1个 (C) 2个 (D) 3个
6、函数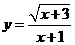 的自变量的取值范围是( )
的自变量的取值范围是( )
(A)x≤3 (B)x≥3 (C)x≤-3且x≠-1 (D) x≥-3且x≠-1
5、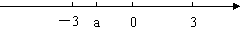 实数a在数轴上对应的点的位置如图所示,化简|a + 3|的结果是( )
实数a在数轴上对应的点的位置如图所示,化简|a + 3|的结果是( )
(A)a + 3 (B) a-3
(C)-a + 3 (D)-a-3
4、下列二次根式中与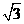 是同类二次根式的是 ( )
是同类二次根式的是 ( )
(A)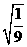 (B)
(B) 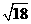 (C)
(C)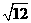 (D)
(D)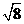
3、三峡电站的总装机容量是一千八百二十万千瓦,用科学记数法把它表示为( )
(A)0.182×108千瓦 (B)1.82×107千瓦 (C) 0.182×10-8千瓦 (D)1.80×10-7千瓦
2、下列等式成立的是( )
(A) x2·x3 = x6 (B) x3 + x3 = x6 (C) (x2)3 = x6 (D) (2x3)2 = 2x6
1、如果水库的水位高于正常水位2m时,记作+2m,那么低于正常水位3m时,应记作( )
(A)+3m (B)-3m (C) +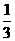 (D) -
(D) -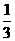
21?(本题满分8分)
计算: 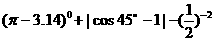
22?(本题满分8分)
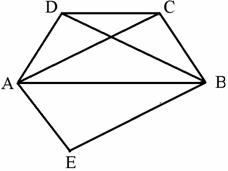 如图,在等腰梯形ABCD中,AB∥CD,AC、BD是对角线,将△ABD沿AB向下翻折到△ABE的位置,试判定四边形AEBC的形状,并证明你的结论.
如图,在等腰梯形ABCD中,AB∥CD,AC、BD是对角线,将△ABD沿AB向下翻折到△ABE的位置,试判定四边形AEBC的形状,并证明你的结论.
23?(本题满分8分)
某校初三(1)班合作学习小组为了了解我市餐饮业人员的收入情况,到某餐厅进行调查.他们将了解到的该餐厅所有10名员工月工资情况列表如下:
|
岗位 |
经理 |
一级厨师 |
二级厨师 |
财务会计 |
服务员 负责人 |
服务员 |
勤杂工 |
|
工资标准(元) |
3000 |
1000 |
900 |
700 |
700 |
500 |
400 |
|
人数 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
(1)请你解答他们设计的下列问题(将答案直接填在横线上):
①该餐厅所有员工的平均工资是 元,所有员工工资的中位数是 元;
②能够较好地反映该餐厅员工工资一般水平的是 ;(填“平均数”或“中位数”)
③去掉经理和勤杂工的工资,其他员工的平均工资是 元.
(2)该合作学习小组的成员们通过比较分析发现,去掉经理和勤杂工的工资后,其他员工的平均工资也能反映该餐厅员工工资的一般水平.从统计理论角度看,当一组数据的个数较少,且可能个别数据变动较大时,常采取去掉其中一个最大值和一个最小值,取其余数值的平均数去描述这组数据集中趋势的方法.现实中采用这种做法的实例较多,请你列举一例.
(要求:所举事例内容健康,符合实际.)
24?(本题满分10分)
如图,反比例函数y= 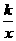 ( k<0)的图象经过点A(-
( k<0)的图象经过点A(-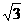 ,m),过A作AB⊥x轴于点B,△AOB的面积为
,m),过A作AB⊥x轴于点B,△AOB的面积为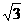 .
.
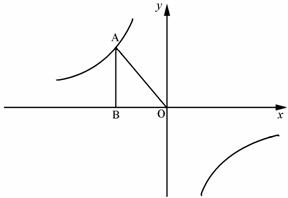 (1)求k和m的值;
(1)求k和m的值;
(2)若过A点的直线y=ax+b与x轴交于C点,且∠ACO=30°,求此直线的解析式.
25?(本题满分10分)
已知关于x的方程(k-3)x2+kx+1=0.
(1)求证不论k取何值,方程总有实数根;
(2)当k=4时,设该方程的两个实数根为α、β,求作一个以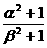 和
和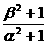 为根的一元二次方程.
为根的一元二次方程.
26?(本题满分12分)
据电力部门统计,每天8︰00至21︰00是用电高峰期,简称“峰时”,21︰00至次日 8︰00是用电低谷期,简称“谷时”.为了缓解供电需求紧张的矛盾,我市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策.具体见下表:
|
时间 |
换表前 |
换表后 |
|
|
峰时(8︰00 - 21︰00) |
谷时(21︰00
- 次日8︰00) |
||
|
电价 |
0.52元/千瓦时 |
x元/千瓦时 |
y元/千瓦时 |
已知每千瓦时峰时价比谷时价高0.25元.小卫家对换表后最初使用的100千瓦时用电情况进行统计分析知:峰时用电量占80%,谷时用电量占20%,与换表前相比,电费共下降2元.
(1)请你求出表格中x和y的值;
(2)小卫希望通过调整用电时间,使她家以后每使用100千瓦时的电费与换表前相比下降10元至15元(包括10元和15元).假设小卫家今后“峰时”用电量占整个家庭用电量的z%,那么,z在什么范围内时,才能达到小卫的期望?
27?(本题满分12分)
如图,AB是半圆⊙O的直径,AC⊥AB,AB=2AC,BF⊥AB,在直径AB上任取一点P(不与端点A、B重合),过A、P、C三点的圆与⊙O相交于除点A以外的另一点D,连结AD并延长交射线BF于点E,连结DB、DP、DC.
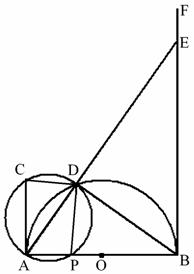 (1)求证:△ACD∽△BPD;
(1)求证:△ACD∽△BPD;
(2)求证:BE=2BP;
(3)试问当点P在何位置时,DE=2AD?
28 (本题满分14分)
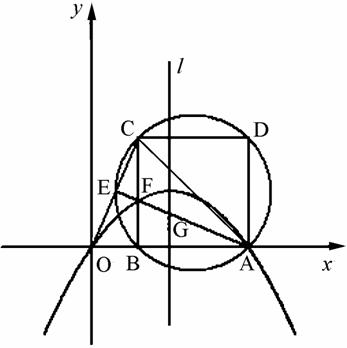
如图,直角坐标系中,已知点A(3,0),B(t,0)( 0<t<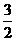 ),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连结AE与BC相交于点F.
),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连结AE与BC相交于点F.
(1)求证:△OBC≌△FBA;
(2)一抛物线经过O、F、A三点,试用t表示该抛物线的解析式;
(3)设题(2)中抛物线的对称轴l与直线AF相交于点G,若G为△AOC的外心,试求出抛物线的解析式;
(4)在题(3)的条件下,问在抛物线上是否存在点P,使该点关于直线AF的对称点在x轴上,若存在,请求出所有这样的点;若不存在,请说明理由.
20.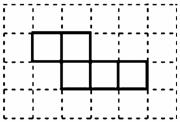 马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com