21、解：测得三个数据：DC=5m，∠α=45°，∠β=47°

　　　　 设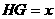　　　　　　　　　　　　　　　　　　　　　　　　　 1分

在Rt△CHG中

　　　　　　　　　　　　　　　　　　　　　　　　　　 3分

在Rt△DHM中

，

∵　　

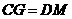
∴　　 　　　　　　　　　　　　　　　　　　　　　5分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

答：铁塔顶端到山底的高为　　　　　　　 　　　　　　　　　　　　8分

20、解：设调价前每件商品的利润是元

　 依题意得：　　　　　　　　　　　　　 3分

整理得：

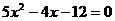
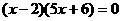
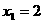
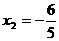　　　　　　　　　　　　　　　　 　　　　　　　5分

经检验 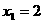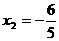，均为方程的根　　　　　　　　　　　　　　　　

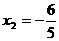不合题意，舍去　　　　　　　　　　　　　　　　　　　　　　 7分

答：调价前每件商品的利润为2元　　　　　　　　　　　　　　　　　　 8分

19、证明，∵∠ACB=90^o，CE⊥AD，∴∠CAD=∠BCF　　　　　　　　　　　 2分

又∵BF∥AC，∴∠FBC=∠DCA=90^o，而AC=BC

∴△FBC≌△DCA

∴FB=CD　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

又∵D是BC的中点，∴CD=DB

故DB=FB，即△DBF为等腰三角形　　　　　　　　　　　　　　　　　　　 6分

又由AC=BC知　　 ∠CAB=∠CBA

BF∥AC知　　 ∠CAB=∠ABF

故∠CBA=∠ABF　　 (说明：此处学生若从　 ∠CBA=∠ABF=　 来论证可酌情给分 )

即AB为等腰三角形DBF的顶角平分线

∴AB垂直平分DF　　　　　　　　　　　　　　　　 　　　　　　　　　　8分

18、解：(1)由题意知，k≠0,且　　　　　　　 2分

　　　　　 　，且　　　　　　　　　　　　　　　　　　 4分

　　　　 (2)不存在　　　　　　　　　　　　　　　　　　　　　　　　 5分

设方程的两个根是,

　　　　　　　　　　　　　　　　　　　　　 　　　　　　6分

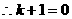，即　　　　　　　　　　　　　　　　　　　　 　

∴满足条件的实数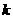不存在。　　　　　　　　　　　　　　　　　　　　　 8分

17、解：

由①得代入②得　　　　 　　　　　　　　　　　　　2分

即　　 　　　　　　　　　　　　　　　　　　　　　　　　4分

得

即原方程组的解为 或　　　　　　　　　　　　　　　 　6分

16、原式　　　　　　　　　　　　　　　　　　　　 3分

　　　　 =5　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

11、6×10⁸;　　 12、　 13、90^o　　 14、　 15、

1、D　　 2、D　　 3、C　 4、D　　 5、A　 6、A　 7、D　 8、D　 9、B　 10、D

22、已知抛物线与轴交于A、B两　　　　　　　　 点，点A在轴的负半轴上，点B在轴的正半轴上，又此抛物线交轴于点C，连AC、BC，且满足△OAC的面积与△OBC的面积之差等于两线段OA与OB的积(即S_△OAC－S_△OBC＝OA·OB).

　 (1)求的值；

　 (2)若tan∠CAB＝，抛物线的顶点为点P，是否存在这样的抛物线，使得△PAB的外接圆半径为？若存在，求出这样的抛物线的解析式；若不存在，请说明理由.

　 解：

初三数学综合测试评分参考

21、下表是小明同学填写实习报告的部分内容：

已知：sin47°＝0.7313，cos47°＝0.6820，tan47°＝1.072，cot47°＝0.9325，请你根据以上的条件，计算出铁塔顶端到山底的高度HG(结果保留两位小数).

　 解：