

题目列表(包括答案和解析)
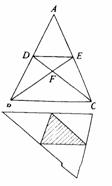
4、已知:如右上图,D、E分别是AB、AC上的点,DC、EB交于F,若AB=AC–AD=AE,则图中共有( )对全等三角形.
A、2 B、3 C、4 D、5
3、已知,直线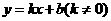 与x轴交点在x轴的正半轴上,有下列结论:
与x轴交点在x轴的正半轴上,有下列结论:
 A、
A、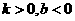 B、
B、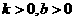 C、
C、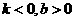 D、
D、 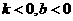
其中正确的有( )个.
A、1 B、2 C、3 D、4
2、两圆直径分别为6和8,圆心距为7,这两个圆的公切线最多有( )条
A、1 B、2 C、3 D、4
1、下列等式成立的是( )
A、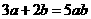 B、
B、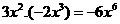
C、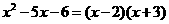 D、
D、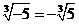
问题:要将一块直径为2m的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面。
操作:
方案一:在图1中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
方案二:在图2中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图)。
探究:
⑴求方案一中圆锥底面的半径;
⑵求方案二中半圆圆心为O,圆柱两个底面圆心为O1、O2,圆锥底面的圆心为O3,试判断以
O1、O2、O3、O为顶点的四边形是什么样的特殊四边形,并加以证明。


(说明:本套试题A卷为毕业卷,共100分;升学为A卷×50% + B卷,共150分)
10、已知:如图1,给出下列6个论断,①AB是⊙O1的直径;②EC是⊙O1的切线;
③AC是⊙O2的直径;④BC·EC=DE·BD;⑤DE∥BC;⑥DE·BC=2CE2。
⑴将6个论断中的3个作为题设,2个论断作为结论,写出一个真命题,并加以证明;
⑵如果AB不是⊙O2直径(如图2),你能否再从其余5 个论断中选取一个论断作为题设,一个论断作为结论,使其成为真命题(不要求证明)。若能,请写出两个;若不能,请你再添加一个条件,写出两个真命题。

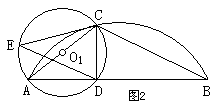
9、某水产品养殖加工厂有200名工人,每名工人每天平均捕捞水产品50千克,或将当日所捕捞的水产品40千克进行精加工。已知每千克水产品直接出售可获利润6元,精加工后再出售,可获利润18元。设每天安排x名工人进行水产品精加工
⑴求每天做水产品精加工所得利润y(元)与x的函数关系式;
⑵如果每天精加工的水产品和未来得及加工的水产品全部出售,那么如何安排生产可使一天所获利润最大?最大利润是多少?
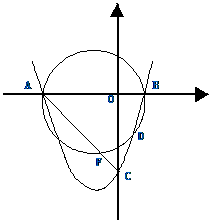
8、如图,抛物线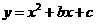 与x轴交于A、B两点,与y轴 交于点C,D是抛物线上一点,其坐标为(
与x轴交于A、B两点,与y轴 交于点C,D是抛物线上一点,其坐标为(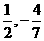 ),B点坐标为(1,0)。
),B点坐标为(1,0)。
⑴求抛物线的解析式;
⑵经过A、B、D三点的圆交AC于F,交直线y = x + 3于点E。试判断△ABC的形状,并加以证明。
7、如图,PA是⊙O的切线,切点为A,PCB是⊙O的割线,交⊙O于C、B两点,半径OD⊥BC,垂足为E,AD交PB于点F,BF=PF。
⑴求证:PA=PF
⑵若CF=1,求切线PA的长。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com