2． 掌握正多边形的定义和有关概念、判定和性质；

1．了解用量角器等分圆周的方法，会用直尺和圆规画圆内接正方形和正多边形；

1)底边为已知线段BC的等腰三角形ABC的顶点A的轨迹是　　　　　　　　

2)以⊙O上一点A为端点的弦的中点的轨迹是　　　　　　　

3)设⊙O_1、⊙O_、2的半径都是r，且O₁ O_、2＞2r，则与⊙O_1、⊙O_、2都外切的圆的圆心的轨迹是　　　　　　

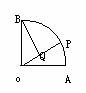4)如图，扇形AOB，OA⊥OB，点P是弧AB上任一点，过B作OP的垂线，垂足为Q，则点Q的轨迹是　　　　　　　　　　　

5)已知线段AO(如图)，(1)以定点O为圆心，定长OA为半径作⊙O；(2)作⊙O的圆内接六边形ABCDEF；(3)作正六边形ABCDEF的内切圆。

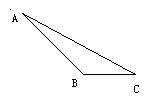
6)已知△ABC(如图)，作△ABC的内切圆。

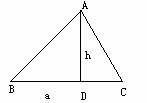
7)已知△ABC，BC=a，高线AD=h(如图)，求作正方形，使其面积等于△ABC面积的2倍。

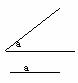
8)用直尺和圆规作一个∠AOB，使∠AOB=30°。

9)已知直线L上一点P以及直线外一点Q(如图)，求作：经过

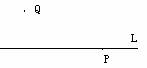点Q且与直线L相切于点P的⊙O。

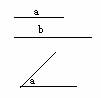10)已知：线段a、b和∠α(如图)，求作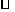：ABCD，使AB=a，

AD=b，∠A=∠α。

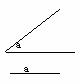11)已知一直角边及与它不相邻的锐角(如图)，限用直尺和圆规

作Rt△。(不写作法，但须保留作图痕迹)

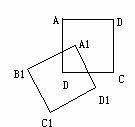
12)如图，两个相同的正方形ABCD和A₁B₁C₁D₁ ，A₁与ABCD的中心重合，且A₁B₁C₁D₁绕A₁转动，试说出它们重叠部分的面积与正方形面积的比。

13)已知等腰三角形的底角和底边(如图)，用直尺和圆规作此三角形(不写作法，但须保留作图痕迹)

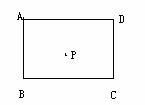
14)如图，在一块矩形的铁皮上有一点P，现要在这块铁皮上剪去一个等腰直角三角形，把它加工成零件，请你在已知矩形ABCD上求作这个等腰直角三角形，使它的直角顶点为P，斜边落在AD上。

5.如图,已知:线段m和角α.求作:等腰三角形ABC,使底角∠B=α,腰AB=m.

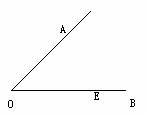
4.如图,已知∠AOB和边OB上一点E,求作:一点P,使P到∠AOB两边的距离相等.且OP=EP

3.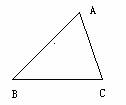如图,已知△ABC,求作 △ABC的外接圆.

2.AB是半径为R的⊙O中的一条弦，若AB 沿点A旋转30°角，那么，AB中点P随之运动所经过路程为(　　 )

A　 πR　　 B　　 R　　　　 C　 πR　　　 D　　 　πR

1.斜边为AB的直角三角形ABC的顶点C的轨迹是　　　　　　　 。

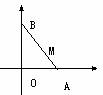
例1．如图，在直角坐标系平面内，线段AB的两端点A、B分别在x轴、y轴的正半轴上滑动，AB=8cm，求线段AB中点M的轨迹。

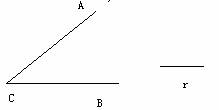
例2．如图，A、B、C三点表示三个村庄，要建一个电视转播站，使它到三个村庄的距离相等，求作电视转播站的位置(要求尺规作图，保留作图痕迹，不写作法和证明)　　　　　　　　　　　　　　

例3．如图，已知：线段r和∠ACB求作一圆O，使它与∠ACB的两边相切，且圆的半径等于r。要求用直尺和圆规作图)

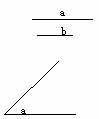
例4．如图，已知线段a、b、∠α，求作：平行四边形ABCD，使BD=a，AC= b，BD、AC的夹角为α。(要求用直尺和圆规作图，保留作图痕迹)

例5．如图，一辆汽车在直线形的公路AB上由A向B行驶，M、N分别是位于公路AB 两侧的村庄。(1)设汽车行驶到公路AB上点P位置时，距离村庄M最近；行驶到点Q位置时，距离村庄N最近。请在图中的公路AB上分别画出点P，Q的位置。(保留作图痕迹)。(2)当汽车从A出发向B行驶时，在公路AB的哪一段路上距离M，N两村庄都越来越近？在哪一段路上距离村庄N越来越近，而离村庄M越来越远？(分别用文字表述你的结论，不必证明)。(3)在公路AB上是否存在这样一点H，使汽车行驶到该点时，与村庄M，N的距离相等？如果存在，请在图中的AB上画出这一点(保留作图痕迹，不必证明)；如果不存在，请简要说明理由。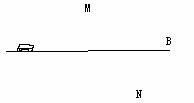

5．和两条已知直线l₁和l₂ 相切的圆的圆心轨迹是　　　　　　　　　 。