1． 已知两圆的半径分别是2和4，圆心距是3，那么这两圆的位置是(　)

　(A)内含　 (B)内切　 (C)相交　 (D) 外切

2．考查两圆位置关系中的相交及相切的性质，可以以各种题型形式出现， 多见于选择题或填空题，有时在证明、计算及综合题申也常有出现。

预习练习：

1．判断基本概念、基本定理等的正误。在中考题申常以选择题或填空题的

形式考查学生对基本概念和基本定理的正确理解，如：已知两圆的半径分别为2、5，且圆心距等于3，则两圆位置关系是 (　　　 )

　　 (A)外离　 (B)外切　 (C)相交　 (D) 内切

4．注意 (1)圆与圆的五种位置关系相交和相切是重点；(2)在解题中把两个圆中有关问题利用圆的性质和直线圆的位置关系的定理和性质转化为一般圆的问题；(3)涉及相交两圆的问题常可作出公共弦，利用圆周角定理及其推论或连心线垂直乎分公共弦。公共弦可沟通两个圆的角之间关系，有了连心线，公共弦不仅可取应用相交两圆的性质定理且还能沟通两圆半径、公切线等之间的关系；(4)涉及相切两圆问题主要可从以下几个方面考虑；①过切点作两圆的公切线，利用弦切角定理或切线长定理；②作出连心线，利用连心线过切点的性质；③利用两圆的圆心距等于两圆半径之和或之差；④当两圆外切时，利用连心线、外公切线及过公切线切点的两条毕径组成的直角梯形，将有关圆的间题转化为直线形间题，把梯形问题转化为直角三角形问题，通过解直角三角形来解决有关两圆公切线等问题。

考查重点与常甩题型：

3．掌握相交两圆的性质和相切两圆的性质;

2．了解两圆位置关系与公共点个数、外公切线条数、内公切线条数以及d、R、r之间的关系;

1．了解两圆公切线的求法，掌握圆和圆的位置关系;

8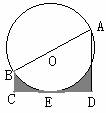． 如图，AB是⊙O直径，CD切⊙O于E，BC⊥CD，AD⊥CD交⊙O于F，∠A＝60°，AB＝4，求阴影部分面积。

7． 如图，PA、PB切⊙O于A、B，若∠APB＝60°，⊙O半径为3，求阴影部分面积。

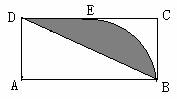
6． 如图，矩形ABCD中，以AB为直径的半圆O切CD于E，AB＝a，

求夹在BD，DE及弧BE间阴影部分面积