3．整式的运算

　　 (1)整式的加减：几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接．整式加减的一般步骤是：

　　 (i)如果遇到括号．按去括号法则先去括号：括号前是“十”号，把括号和它前面的“+”号去掉。括号里各项都不变符号，括号前是“一”号，把括号和它前面的“一”号去掉．括号里各项都改变符号．

　　 (ii)合并同类项： 同类项的系数相加，所得的结果作为系数．字母和字母的指数不变．

　　 (2)整式的乘除：单项式相乘(除)，把它们的系数、相同字母分别相乘(除)，对于只在一个单项式(被除式)里含有的字母，则连同它的指数作为积(商)的一个因式相同字母相乘(除)要用到同底数幂的运算性质：

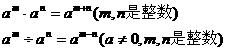
　　 多项式乘(除)以单项式，先把这个多项式的每一项乘(除)以这个单项式，再把所得的积(商)相加．

　　 多项式与多项式相乘，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．

　　 遇到特殊形式的多项式乘法，还可以直接算：

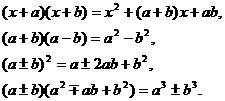
　　 (3)整式的乘方

　　 单项式乘方，把系数乘方，作为结果的系数，再把乘方的次数与字母的指数分别相乘所得的幂作为结果的因式。

　　 单项式的乘方要用到幂的乘方性质与积的乘方性质：

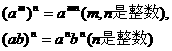
　　 多项式的乘方只涉及

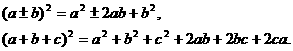
考查重点与常见题型

2．整式的有关概念

　　 (1)单项式：只含有数与字母的积的代数式叫做单项式．

　　 对于给出的单项式，要注意分析它的系数是什么，含有哪些字母，各个字母的指数分别是什么。

　　 (2)多项式：几个单项式的和，叫做多项式

对于给出的多项式，要注意分析它是几次几项式，各项是什么，对各项再像分析单项式那样来分析

(3)多项式的降幂排列与升幂排列

　　 把一个多项式技某一个字母的指数从大列小的顺序排列起来，叫做把这个多项式按这个字母降幂排列

　　 把-个多项式按某一个字母的指数从小到大的顺斤排列起来，叫做把这个多项式技这个字母升幂排列，

　　 给出一个多项式，要会根据要求对它进行降幂排列或升幂排列．

　　 (4)同类项

所含字母相同，并且相同字母的指数也分别相同的项，叫做同类顷．

　　 要会判断给出的项是否同类项，知道同类项可以合并．即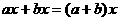　　　　　　　　　 其中的X可以代表单项式中的字母部分，代表其他式子。

1．代数式的有关概念．

　　 (1)代数式：代数式是由运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连结而成的式子．单独的一个数或者一个字母也是代数式．

　　 (2)代数式的值；用数值代替代数式里的字母，计算后所得的结果p叫做代数式的值．

　　 求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值．

(3)代数式的分类

5、　 掌握整式的加减乘除乘方运算，会进行整式的加减乘除乘方的简单混合运算。

考查重点

4、　 能熟练地运用乘法公式(平方差公式，完全平方公式及(x+a)(x+b)=x²+(a+b)x+ab)进行运算；

3、　 掌握同底数幂的乘法和除法、幂的乘方和积的乘方运算法则，并能熟练地进行数字指数幂的运算；

2、　 理解整式、单项式、多项式的概念，会把多项式按字母的降幂(或升幂)排列，理解同类项的概念，会合并同类项；

1、　 了解代数式的概念，会列简单的代数式。理解代数式的值的概念，能正确地求出代数式的值；

10．已知：如图，AD切⊙O于点D，ACB为⊙O的割线，AP＝AD，BP,CP分别交⊙O于M,N，求证：(1)△PCA∽△ABP　 (2)MN∥AP.

9．如图，AB是⊙O直径，BC是弦，CD切⊙O于C，AD⊥CD交BC延长线于E，AE＝8cm，求AB的长。