3．二次根式的运算

　　 (1)二次根式的加减

　　 二次根式相加减，先把各个二次根式化成最简二次根式，再把同类三次根式分别合并．

　　 (2)三次根式的乘法

　　 二次根式相乘，等于各个因式的被开方数的积的算术平方根，即

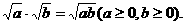
　　 二次根式的和相乘，可参照多项式的乘法进行．

　　 两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，那么这两个三次根式互为有理化因式．

　　 (3)二次根式的除法

　　 二次根式相除，通常先写成分式的形式，然后分子、分母都乘以分母的有理化因式，把分母的根号化去(或分子、分母约分)．把分母的根号化去，叫做分母有理化．

[考查重点与常见题型]

2．二次根式的性质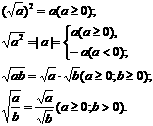　　

1．二次根式的有关概念

　　 (1)二次根式

　　 式子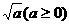叫做二次根式．注意被开方数只能是正数或O．

　　 (2)最简二次根式

　　 被开方数所含因数是整数，因式是整式，不含能开得尽方的因数或因式的二次根式，叫做最简二次根式．

　　 (3)同类二次根式

　　 化成最简二次根式后，被开方数相同的二次根式，叫做同类二次根式．

3.掌握二次根式的运算法则，能进行二次根式的加减乘除四则运算，会进行简单的分母有理化。

内容分析

2.了解二次根式、最简二次根式、同类二次根式的概念，会辨别最简二次根式和同类二次根式。掌握二次根式的性质，会化简简单的二次根式，能根据指定字母的取值范围将二次根式化简；

1.理解平方根、立方根、算术平方根的概念，会用根号表示数的平方根、立方根和算术平方根。会求实数的平方根、算术平方根和立方根(包括利用计算器及查表)；

4．解关于x的方程x²+x – 2+k(x²+2x)=0　 (对k要讨论)

3．解方程

(1) (2x – 3)² = (3x – 2)²　　　　　 (2) 　-= x+2　　　　

　(3)　 (1+)x² –(3 +　)x+　 =0　 　(4) 5m² – 17m + 14=0

　(5)　 (x² +x+1)(x² +x + 12)=42　　　　 (6) 2x² + (3a-b)x –2a²+3ab- b² =0

2．已知关于x的一元二次方程 (a x + 1 ) ( x – a ) = a – 2 的各项系数之和等于3, 求这时方程的解

1．已知实数a.b.c满足 +│b+1│+(c + 3)² = 0 求方程ax²+bx+c=0的根