26. (本题11分)

　　 如图，H是⊙O的内接锐角△ABC的高线AD、BE的交点，过点A引⊙O的切线，

与BE的延长线相交于点P，若AB的长是关于x的方程

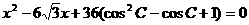的实数根。

　　 (1)求：∠C=　　　 度；AB的长等于　　　 (直接写出结果)。

　　 (2)若BP=9，试判断△ABC的形状，并说明理由。

25. (本题11分)

　　 织里某童装加工企业今年五月份工人每人平均加工童装150套，最不熟练的工人加工的童装套数为平均套数的60%。为了提高工人的劳动积极性，按时完成外商订货任务，企业计划从六月份起进行工资改革。改革后每位工人的工资分二部分：一部分为每人每月基本工资200元；另一部分为每加工1套童装奖励若干元。

　　 (1)为了保证所有工人的每月工资收入不低于市有关部门规定的最低工资标准450元，按五月份工人加工的童装套数计算，工人每加工1套童装企业至少应奖励多少元(精确到分)？

　　 (2)根据经营情况，企业决定每加工1套童装奖励5元。工人小张争取六月份工资不少于1200元，问小张在六月份应至少加工多少套童装？

24. (本题10分)

　　 已知如图，直线y=-2x+2与x轴、y轴分别交于点A、B，以线段AB为直角边在第一象限内作等腰直角△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D。

　　 (1)求点A、B的坐标和AD的长。

　　 (2)求过B、A、D三点的抛物线的解析式。

23. (本题10分)

　　 某校初三(1)班36位同学的身高的频数分布直方图如图所示。

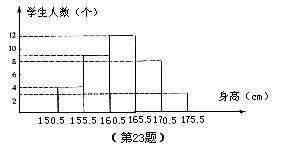
　　 问：(1)身高在哪一组的同学最多？

　　　　 (2)身高在160cm以上的同学有多少人？

　　　　 (3)该班同学的平均身高约为多少(精确到0.1cm)？

22. (本题9分)

　　 解方程：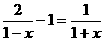

21. (本题9分)

　　 计算：(-1)⁰+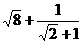

20. 如图，在半径为9，圆心角为90°的扇形OAB的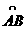上有一动点P，PH⊥OA，垂足为H，设G为△OPH的重心(三角形的三条中线的交点)，当△PHG为等腰三角形时，PH的长为　　　　 。

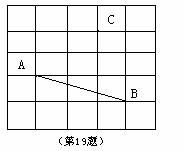
19. 如图，已知图中每个小方格的边长为1，则点C到AB所在直线的距离等于　　　 。

18. 已知如图，在△ABC中，BC=8，AB的中垂线交BC于D，AC的中垂线交BC与E，则△ADE的周长等于　　　　　　 。

17. 已知梯形的中位线长为6，下底长为9，则该梯形上底的长为　　　　　 。