26. 已知：抛物线y=ax²+4ax+t与x轴的一个交点为A(-1，0)(1)求抛物线与x轴的另一个交点B的坐标； (2)D是抛物线与y轴的交点，C是抛物线上的一点，且以AB为一底的梯形ABCD的面积为9，求此抛物线的解析式；(3)E是第二象限内到x轴，y轴的距离 的比为5：2的 点，如果点E在(2)中的抛物线上，且它与点A在此抛物线对称轴的同侧，问 ：在抛物线的对称轴上是否存在点P， 使的周长最小？若存在，求出点P的坐标，若不存在，请说明理由。

　　 解：

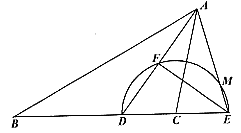　25. 已知：在ΔABC中，AD为∠BAC的平分线，以C为圆心，CD为半径的半圆交BC的延长线于点E，交AD于点F，交AE于点M，且

∠B=∠CAE,FE∶FD=4∶3。

　 (1)求证：AF=DF.

　 (2)求∠AED的余弦值；

　 (3)如果BD=10，求ΔABC的面积。

24. 已知：关于x的方程x²-2mx+3m=的两个实数根是x₁,x₂，且(x₁-x₂)²=16。如果关于x的另一个方程x²-2mx+6m-9=0的两个实数根都在x₁和x₂之间，求m的值。

　　 解：

23. 列方程或方程组解应用题：

　 在社会实践活动中，某校甲、乙、丙三位同学一同调查了高峰时段北京的二环路、三环路、四环路的车流量(每小时通过观测点的汽车车辆数) ，三位同学汇报高峰时段的车流量情况如下：

　　 甲同学说：“二环路车流量为每小时10000辆”；

　　 乙同学说：“四环路比三环路车流量每小时多2000辆”；

　　 丙同学说：“三环路车流量的3倍与四环路车流量的差是二环路车流量的2倍”。

　　 请你根据他们所提供的信息，求出高峰时段三环路、四环路的车流量各是多少。

　　 解：

22.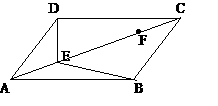 如图，在平行四边形ABCD中，点E、F在对角线AC上，且AE=CF。请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可)。

　 (1)连结___________

　 (2)猜想：__________=__________。

　 (3)证明：

21. (6分)用换元法解方程x²-3x+5+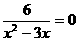

解：

20. (4分)计算：。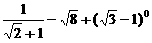

解：

19. (4分)分解因式：x²-2xy+y²-9。

解：

18. 观察下列顺序排列的等式：

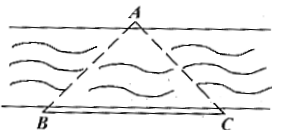
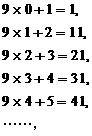
　　 猜想：第n个等式(n为正整数)应为___________________。

17. 如图，B、C是河岸边两点，A是对岸岸边一点，测得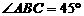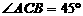，，BC=60米，则点A到岸边BC的距离是________米。