
题目列表(包括答案和解析)
25、(本题满分8分)
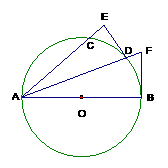 如图AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F。
如图AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F。
1) 求证:DE是⊙O的切线。
2) 若DE=3,⊙O的半径是5,求BF的长。
24、(本题满分8分)
某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其它生产条件不变,因此每增加一台机器,每台机器平均每天将少生产4件产品。
1) 如果增加x台机器,每天的生产总量为y件,请写出y与x的函数关系式。
2) 增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?
23、(本题满分8分)四边形是我们大家最熟悉的图形之一,我们已经发现了它的许多性质,只要善于观察、乐于探索,我们还会发现更多的结论。
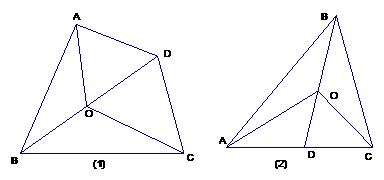
1)四边形的一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图1)其中相对的两个三角形的面积之积相等,你能够证明这个结论吗?试试看。
已知:四边形ABCD中,O是对角线BD上任意一点,(图1)
 求证:
求证: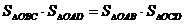
2)在三角形中(如图2),你能否归纳出类似的结论,若能够,写出你猜想的结论,并证明;若不能够,说明理由。
22、(本题满分8分)
 已知:在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q。
已知:在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q。
1) 求四边形AQMP的周长。
2) 写出图中的两对相似三角形(不需证明)。
3) M位于BC的什么位置时,四边形AQMP为菱形?
说明你的理由。
21、(本题满分6分)
某市今年1月1日起调整居民用水价格,每立方米水费上涨25%。小明家去年12月份的水费是18元,而今年5月份的水费是36元。已知小明家今年5月份的用水量比去年12月份多6m3,求该市今年用水的价格。
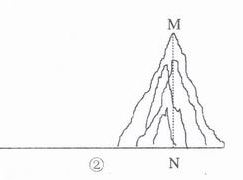
20、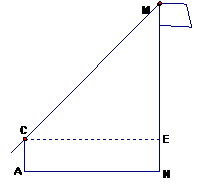 (本题满分6分)在一次实践活动中,某课题学习小组用测倾器、皮尺测量旗杆的高度,他们设计了如下的方案(如图1所示):
(本题满分6分)在一次实践活动中,某课题学习小组用测倾器、皮尺测量旗杆的高度,他们设计了如下的方案(如图1所示):
(1) 在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α ;
(2) 量出测点A到旗杆底部N的水平距离AN=m;
(3) 量出测倾器的高度AC=h。
根据上述测量数据,即可求出旗杆的高度MN。
如果测量工具不变,请仿照上述过程,设计一个测量
某小山高度(如图2)的方案:
1) 在图2中,画出你测量小山高度MN的示意图
(标上适当的字母)
2)写出你的设计方案。 (图1)
19、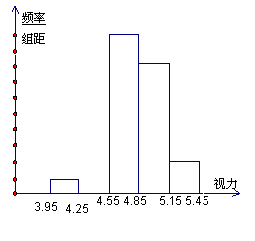 (本题满分6′)青少年视力水平下降已经引起全社会的广泛关注,为了了解某市初中毕业生5000名学生的视力情况,我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图(部分):
(本题满分6′)青少年视力水平下降已经引起全社会的广泛关注,为了了解某市初中毕业生5000名学生的视力情况,我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图(部分):
|
分组 |
频数 |
频率 |
|
3.95-4.25 |
2 |
0.04 |
|
4.25-4.55 |
8 |
0.16 |
|
4.55-4.85 |
|
0.40 |
|
4.85-5.15 |
16 |
0.32 |
|
5.15-5.45 |
4 |
0.08 |
|
合计 |
|
1 |
①.根据上述数据,补全频率分布表与频率分布直方图
②.若视力在4.85以上属于正常,不需要矫正,试估计该市5000名初中毕业学生中约有多少名学生的视力需要矫正?
18、本小题满分6分
已知方程5x2+kx-10=0的一个根是-5,求它的另一个根及k的值。
17、如图,AB、CD是两条相互垂直的公路,设计时想在拐弯处用一段圆弧形湾道把它们连接起来(圆弧在A、C两点处分别与道路相切),测得AC=60米,∠ACP=45°。
(1) 在图中画出圆弧形弯道的示意图;
(2) 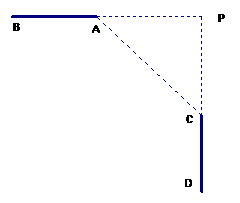 求弯道部分的长。(结果保留四个有效数字)
求弯道部分的长。(结果保留四个有效数字)
16、观察下列由棱长为1的小立方体摆成的图形,寻找规律:
如图1中:共有1 个小立方体,,其中1个看得见,0个看不见;如图2中:共有8个小立方体,其中7个看得见,1个看不见;如图3中:共有27个小立方体,其中有19个看得见,8个看不见;……,则第6个图中,看不见的小立方体有 个。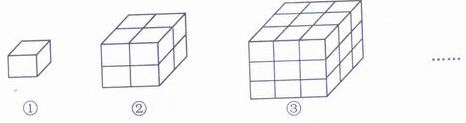
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com