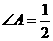
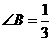
2．已知：四边形ABCD中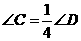，，求：四边形ABCD的四个内角的度数．

1．指出下列图4-1中四边形的个数．

图4-1

4．作图题：根据下列条件分别作四边形ABCD．

　(1)AB＝3cm，BC＝2cm，CD＝1.5cm，∠ABC＝45°，∠BCD＝120°；

　(2)AB＝6cm，BC＝8cm，∠A＝120°，∠B＝60°，∠D＝90°．

综合练习

3．已知：四边形的四个外角之比为1∶2∶3∶4．求：这个四边形的四个内角的度数．

2．已知：在四边形ABCD中，∠A＝∠C，∠B＝∠D，求∠A+∠B的度数．

1．已知：在四边形ABCD中，∠A∶∠B∶∠C∶∠D＝1∶2∶3∶3．求∠A、∠B、∠C、∠D的度数．

(四)与梯形一腰中点有关的对角线．

(7)连结梯形一顶点及一腰中点．如图2(h)，若E为DC中点，连结AE并延长，交BC延长线于F，则△ADE≌△FCE，S△ABF=S梯形ABCD，△ABF中包含梯形一腰AB，上、下底之和BF＝BC+AD和一底角∠B．

(8)过一腰中点作另一腰平行线．如图2(i)，若E为DC中点，过E作FG∥AB，交AD延长线于F，交BC于G，则△DEF≌△CEG，S梯形ABCD＝，ABGF中包含梯形的一腰AB与两底角．

预习练习

1．　 梯形两底的差是4，中位线长是8，则上底是　　，下底长是　　。

2．　 等腰梯形有一个角是60°，上下底长分别是2cm和6cm，则腰长为　　 。

3．　 若梯形的中位线被它的两条对角线三等分，则梯形的上底a与下底b(a<b)的比是(　)

(A)　　　(B)　　　　　(C)　　　　(D)

4．　 直角梯形一腰长10cm，则一条腰与底边所成的角是30°，则另一腰长为　　　　 cm。

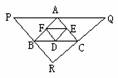
5．　 等腰梯形ABCD中，AD∥BC，(1)如果延长BA和CD相交于E，则EA＝　　　，(2)如果作AF∥DC交BC于F，则⊿ABF是　　　　　 三角形，四边形ADCF是　　　　　 形。(3)如果作AG⊥BC于G，DH⊥BC于H，则BG＝　　　　 ＝　　　　　　，(4)如果作DK∥AC交BC的延长线于K，则DK＝　　　　　 ＝　　　　　　　 。

基础复习

1.下面四个命题中，错误的命题个数是(　　 )

　　 (1)有一组对边平行的四边形是梯形

　　 (2)有一个角是直角的梯形是直角梯形

　　 (3)有两个角相等的梯形是等腰梯形

　　 (4)两条对角线相等的梯形是等腰梯形

(A)1　　 (B)2　　 (C)3　　 (D)0

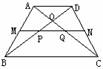
2.如图，梯形ABCD中，AD∥BC，M，N分别是AB，CD的中点，AD＝4，BC＝6，则MN=　　　　　 ，PQ=　　　　　 ，S_△AOD：S_△BOC=　　　　　 .

3.如图，△ABC的周长为18cm，面积为36cm2，它的三条中位线组成的新三角形DFE的周长为　　 　　，面积为　　　　　 ，分别过A、B、C作对边的平行线相交组成△PQR　　 周长为　　　　　 ，面积为　　　　　 .

典型例题

1．如图，矩形ABCD中，AC，BD交于O点，BE⊥AC于E，CF⊥BD于F，且∠CDF＝60°，CF＝cm。(1)求证四边形BCFE是等腰梯形；(2)求这个梯形的中位线长。

2．如图，梯形ABCD中，AD∥BC，∠B+∠C＝90°，E，F分别是AD，BC的中点，求证EF＝(BC－AD)

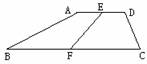
3. 如图，梯形ABCD中，AD∥BC，∠A=90°，E是AB上一点，EC＝ED，∠BEC＝75°，∠AED＝45°，求证AB＝BC。

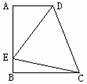
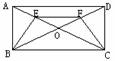
4. 如图，在等腰梯形ABCD中，AB∥DC，CG⊥AB于G，对角线AC⊥BC于点O，EF是中位线，求证CC＝EF.

课堂练习

1．顺次连接等腰梯形两底及两对角线的中点所得的四边形足(　　 )

　 (A)平行四边形　　 (B)矩形　　 (C)菱形　　 (D)正方形

2. 直角梯形的一条对角线把梯形分成两个三角形，其中一个是边长为30的等边三角形，则这个梯形的中位线长是(　　 )

　 (A)15　　 (B)22.5　　 (C)45　　 (D)90

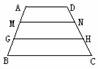
3. 如图，梯形ABCD中，AD∥MN∥GH∥BC，AM＝MG＝GB，AD＝12，BC＝28，

则MN十GH＝(　　 )

　 (A)30　　 (D)38　　 (C)40　　 (D)46

4．梯形ABCD中，AD∥BC，AB=CD，BD平分∠ABC，BD⊥CD，延长BA，CD交于E点，则∠E的度数是　　　　　

5.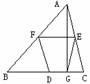 如图，△ABC中，D，F，F分别是各边中点，AG⊥BC于G。

求证：四边形DGEF是等腰梯形

6. 梯形ABCD中，AD∥BC，∠B＝50°，∠C＝80°，求证：AD+DC=BC

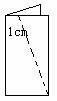
课外训练

1. 等腰梯形的腰与中位线的长都是6厘米，则它的周长是　　　　　 厘米

2. 如图，把长为10cm的长方形纸片对折，按图中的虚线剪成梯形并打开，

则打开后，梯形中位线的长＝　　　　　 cm

3. 直角梯形ABCD中，∠D＝90°，AD＝3，CD＝4，且CA⊥AB，则BC＝　　　　 ，梯形面积是　　　　　

4. 等腰梯形的两条对角线分别垂直于两腰，一底边等于腰，则梯形上底：下底＝　　

5.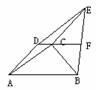 等腰梯形的腰长是24厘米，一对角线分中位线成8厘米和20厘米，则此对角线长为　　 厘米．

6. 如图，梯形ABCD中，AB是下底，以AD，AC为邻边作ADEC，

延长DC交BE于F点。求证F是BE的中点

7. 梯形ABCD中，AD∥BC，AD+BC=AB，F为CD中点，求证:AF⊥BF

8. 如图，梯形ABCD中，AB∥CD，AD=BC，设AB＝a，DC＝b，BC=c,

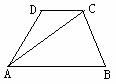　AC＝m。求证：m²＝c²+ab

(三)与对角线有关的辅助线．

(5)连接对角线．如图2(f)，连结AC，BD交于O，则S△ABC=S△DBC，S△BAD＝S△CAD，S△AOB=S△DOC．

(6)平移对角线．如图2(g)，作DE∥AC，交BC延长线于E，则△DBE中包含梯形的两条对角线BD，DE及梯形上、下底之和BE=BC+AD，△BDE与梯形ABCD有共同的高DF和面积．

(二)与高有关的辅助线．

(4)图2(e)，作AE⊥BC于E，DF⊥BC于F，则BE+CF=BC-AD．

(一)与腰有关的辅助线．

(1)梯形内平移一腰．如图2(b)，作AE∥DC交BC于E，则△ABE中包含梯形的两腰AB和AE，两底角的度数∠B，∠AEB和两底边之差BE＝BC-AD．

(2)梯形外平移一腰．如图2(c)，作CE∥BA交AD延长线于E，EABC中包含梯形的一底、一腰、两底角．

(3)延长两腰．如图2(d)，分别延长BA，CD交于E，△BEC中包含梯形的两个底角和下底．