25. (本小题满分14分)

如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为(3，0)，(3，4)。动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥AC，交AC于P，连结MP。已知动点运动了x秒。

(1)P点的坐标为(　　　　　　 ，　　　　　　　 )；(用含x的代数式表示)

(2)试求 ⊿MPA面积的最大值，并求此时x的值。

(3)请你探索：当x为何值时，⊿MPA是一个等腰三角形？

你发现了几种情况？写出你的研究成果。

24. (本小题满分14分)

如左图，正方形 ABCD的边长为2厘米，点E从点A开始沿AB边移动到点B，点F从点B开始沿BC边移动到点C，点G从点C开始沿CD边移动到点D，点H从点D开始沿DA边移动到点A、它们同时开始移动，且速度均为 0.5厘米/秒.设运动的时间为t(秒)

(1)求证：△HAE≌△EBF

(2)设四边形EFGH的面积为S(平方厘米)，求S与t之间的函数关系式，并写出自变量t的取值范围；

( 3 )在下图中用描点法画出(2)中函数的图象，并观察图象，答出t为何值时，四边形EFGH的面积最小？最小值是多少？

23. (本小题满分12分)

某汽车停车场预计“十·一”国庆节这天将停放大小汽车1200辆次，该停车场的收费标准为：大车每辆次10元，小车每辆次5元.根据预计，解答下面的问题：

⑴　写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式，并指出自变量的取值范围；

⑵　如果国庆节这天停放的小车辆次占停车总辆次的65%-85%，请你估计国庆节这天该停车场收费金额的范围.

22. (本小题满分12分)

如图，在□ABCD的纸片中，AC⊥AB，AC与BD相交于O，将△ABC沿对角线AC翻转

180°，得到△AB′C.

(1)求证：以A、C、D、B′为顶点的四边形是矩形；

(2)若四边形ABCD的面积S＝12cm². 求翻转后纸片重叠部分的面积，即S_△ACE.

21、(本小题满分12分)

2006年广州市春季房交会期间，某公司对参加本次房交会的消费者进行了随机的问卷调查，共发放1000份调查问卷，并全部回收.根据调查问卷，将消费者年收入情况整理后，制成表格一；将消费者打算购买住房的面积的情况整理后，制成表格二，并作出部分频率分布直方图(如图9)

　 表格一(被调查的消费者年收入情况)

　 表格二(被调查的消费者打算购买住房的面积的情况，注：住房面积取整数)

请你根据以上信息，回答下列问题：

⑴根据表一可得，被调查的消费者平均年收入为　　　 　　　万元；被调查的消费者年收入的中位数是　　　　　 万元；在平均数、中位数这两个数中，　　　　　 更能反映出被调查的消费者年收入的一般水平.

⑵根据表二可得，打算购买100.5-120.5平方米房子的人数是　　　　　 人；打算购买住房面积不超过100平方米的消费者的人数占被调查人数的百分数是　　　　　 .

⑶在图9中补全这个频率分布直方图.

20. (本小题满分10分)

如图，广州某公园入口处原有三阶台阶，每级台阶高为20cm,深为30cm.为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度。 (精确到1 cm)

19．(本小题满分10分)

已知:如图,A、F、C、D四点在一直线上，AF＝CD，AB∥DE，且AB＝DE．

求证：⑴△ABC≌△DEF；

⑵∠CBF＝∠FEC.

18. (本小题满分9分)

解方程：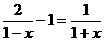

17. (本小题满分9分)

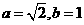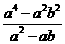当时，求的值

16、不等式组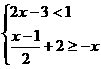的解集为______________