25．(成都市)已知：如图，在半径为r的半圆O中，半径OA⊥直径BC，点E与点F分别在弦AB、AC上滑动并保持AE＝CF，但点F不与A、C重合，点E不与B、A重合．

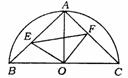
　(1)求证：S_{四边形AEOF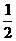}＝r²；

　(2)设AE＝x，S_△OEF＝y，写出y与x之间的函数解析式，并求出自变量x的取值范围；

　(3)S_△OEF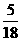＝ S_△ABC时，求点E、F分别在AB、AC上的位置及E、F两点间的距离．

24．(成都市)已知抛物线y＝x²和直线y＝(m²－1)x+m²．

　(1)当m为何实数时，抛物线与直线有两个交点？

　(2)设坐标原点为O，抛物线与直线的交点从左至右分别为A、B，当抛物线与直线两交点的横坐标之差为3时，求三角形AOB中OB边上的高．

23．(成都市)如图，Rt△ABO的顶点A是双曲线y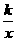＝与直线y＝－x－(k+1)在第二象限的交点，AB⊥x轴于B，且S_△ABO＝．

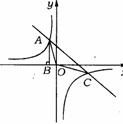
　(1)求这两个函数的解析式；

　(2)求直线与双曲线的两个交点A、C的坐标和△ABC的面积．

22．(成都市)计算：2sin45°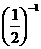－－ |－tan60°| +．

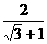21．(长沙市)计算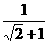：+(+1)⁰－2sin45°．

20．(福州市)已知：矩形ABCD在平面直角坐标系中，顶点A、B、D的坐标分别为A(0，0)，B(m，0)，D(0，4)，其中m≠0．

　(1)写出顶点C的坐标和矩形ABCD的中心P点的坐标(用含m的代数式表示)；

　(2)若一次函数y＝kx－1的图象l把矩形ABCD分成面积相等的两部分，求此一次函数的解析式(用含m的代数式表示)：

　(3)在(2)的前提下，l又与半径为1的⊙M相切，且点M(0，1)，求此时矩形ABCD的中心P点的坐标．

19．(江西省)已知抛物线y＝－x²+bx+c与x轴的两个交点分别为A(m，0)，B(n，0)，且m+n＝4，＝．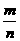

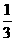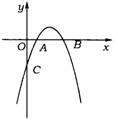
　(1)求此抛物线的解析式；

　(2)设此抛物线与y轴的交点为C，过C作一条平行于x轴的直线交抛物线于另一点P，求△ACP的面积S_△ACP．

18．(安徽省)求直线y＝3－x与圆x²+y²＝5的交点的坐标．

17．(山东省)已知直线y＝x+4与x轴、y轴的交点分别为A、B．又P(0，－1)Q(0，k)，其中0＜k＜4．再以Q点为圆心，PQ的长为半径作圆，则当k取何值时，⊙Q与直线AB相切？

16．(甘肃省)如图，在△ABC中，AB＝4，BC＝3，∠B＝90°，点D在AB上运动，但与A、B不重合，过B、C、D三点的圆交AC于E，连结DE．

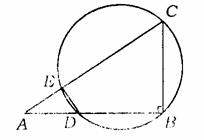
　(1)设AD＝x，CE＝y，求y与x之间的函数关系式，并指出自变量x的取值范围；

　(2)当AD长为关于x的方程2x²+(4m+1)x+2m＝0的一个整数根时，求m的值．