
题目列表(包括答案和解析)
5. 如图所示的四个图被称作平面图。
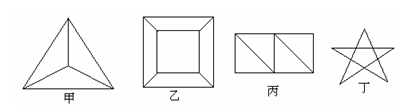
⑴数一数每个图形中各有多少个顶点,多少条边,这些边围出了多少个互不重叠的区域,将结果填入下表
|
图 |
顶点个数(A) |
边数(N) |
区域数(M) |
|
甲 |
|
|
|
|
乙 |
|
|
|
|
丙 |
|
|
|
|
丁 |
|
|
|
⑵观察上表,推断平面图的顶点A、边数N、区域数M之间的关系式;
⑶现已知某一个平面图有1001个顶点和1001个区域,试根据中推断出的关系式,确定这个图案有多少条边。
4.
(格点问题)用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形。设格点多边形的面积为S,它各边上格点的个数和为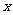 。
。
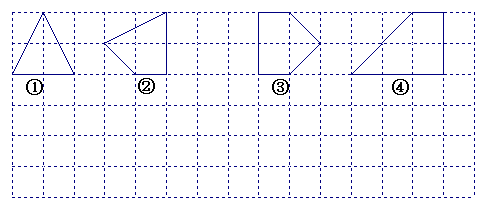
(1)上图中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出S与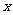 之间的关系式。
之间的关系式。
答:S= 。
|
多边形的序号 |
① |
② |
③ |
④ |
… |
|
多边形的面积S |
2 |
2.5 |
3 |
4 |
… |
各边上格点的个数和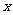 |
4 |
5 |
6 |
8 |
… |
(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有2格点。此时所画的各个多边形的面积S与它各边上格点的个数和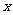 之间的关系式是:S=
。
之间的关系式是:S=
。
(3)请你继续探索,当格点多边形内部有且只有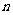 个格点时,猜想S与
个格点时,猜想S与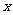 有怎样的关系?答:S=
。
有怎样的关系?答:S=
。
2.
我们知道,用尺规不能三等分角,借助如图所示的双曲线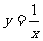 ,便可以三等分一个角了。
,便可以三等分一个角了。
(1)请你按照下面的步骤做出∠AOB的三等分线OM(图中OA与双曲线的交点为P);
①以P为圆心,以2OP为半径作弧交双曲线于R(R在∠AOB内部);②过点P作x轴的平行线,过点R做y轴的平行线,两直线相交于点M;再过点P作y轴的平行线,过点R做x轴的平行线,两直线相交于点N;③连接OM。
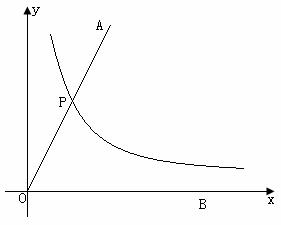 (2)设点P、R的横坐标分别为p、r,求直线OM 的解析式,并判断点N是否在直线OM上(说明理由);
(2)设点P、R的横坐标分别为p、r,求直线OM 的解析式,并判断点N是否在直线OM上(说明理由);
(3)证明:直线OM是∠AOB的三等分线。
27. 解: (1)据题意知: A(0, -2), B(2, -2)
∵A点在抛物线上, ∴C=-2
∵12a+5c=0,
∴a=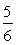
由AB=2知抛物线的对称轴为: x=1
即: 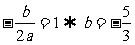
∴抛物线的解析式为: 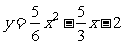 ……………………3分
……………………3分
(2)①由图象知: PB=2-2t, BQ= t
∴S=PQ2=PB2+BQ2=(2-2t)2 + t2
即 S=5t2-8t+4 (0≤t≤1) ……………………………………5分
②∵S=5t2-8t+4 (0≤t≤1)
∴S=5(t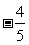 )2 +
)2 +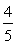 (0≤t≤1)
(0≤t≤1)
∴当t=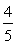 时, S取得最小值
时, S取得最小值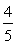 . …………………………………6分
. …………………………………6分
假设存在点R, 可构成以P、B、R、Q为顶点的平行四边形.
这时PB=2 =0.4, BQ=0.8, P(1.6,
-2), Q(2, -1.2)
………7分
=0.4, BQ=0.8, P(1.6,
-2), Q(2, -1.2)
………7分
a、过Q作QR∥BP交抛物线于R。
当y=-1.2时,x1=2.4,x2=-0.4
∴R1(2.4,-1.2),R2(-0.4,-1.2)
∴QR1=0.4, QR1=2.4
∵BP=0.4
∴QR1=BP, QR2≠BP
此时有QR1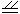 PB,则四边形BPQR为平行四边形.
PB,则四边形BPQR为平行四边形.
∴R的坐标为(2.4, -1.2) …………………………9分
b、过P作PR∥BQ交抛物线于R。
当x=1.6时,y=-2.4
∴R(1.6,-2.4)
∴PR=0.4
∵BQ=0.4
∴PR=BQ
此时有PR 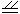 BQ,则四边形BQPR为平行四边形.
BQ,则四边形BQPR为平行四边形.
∴R的坐标为(1.6,-2.4) …………………………11分
c、过B作BR∥PQ交抛物线于R。
直线PQ:y=2x-5.2
直线BR:y=2x-6
则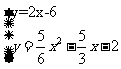 解得x1=2,x2=2.4
解得x1=2,x2=2.4
∴另一交点为(2.4,-1.2)
此时QR≠PB
则四边形BQPR不是平行四边形. …………………………12分
26、(1)证明: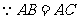 ,
,
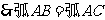
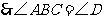 .
.
又 ,
,
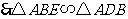 .
………………………3分
.
………………………3分
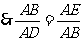 .
.
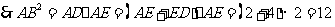 .
.
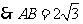 .
……………………………………5分
.
……………………………………5分
(2)直线 与
与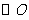 相切.
……………………………………6分
相切.
……………………………………6分
连接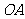 .
.
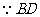 为
为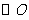 的直径,
的直径,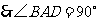 .
.
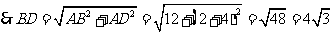 .
.
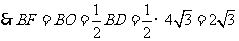 .
.
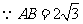 ,
,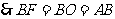 .
.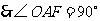 .
.
 直线
直线 与
与 相切.
…………………9分
相切.
…………………9分
25、(1) △ABC和△ABP、△AOC和△ BOP、△CPA和△CPB ; ………3分
(2) △ABP , 因为平行线间的距离相等,所以无论点P在m上移动到任何位置,总有△ABP与△ABC同底等高,因此,它们的面积总相等. ; …5分
(3)方案设计及理由:
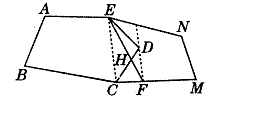 连接EC,过点D作DF∥EC,交CM于点F,连接EF,
连接EC,过点D作DF∥EC,交CM于点F,连接EF,
EF即为所求直路位置.
设EF交CD于点H,由上面得到的结论可知:
SΔECF=SΔECD,SΔHCF=SΔEDH,所以S五边形ABCDE=
S五边形ABCFE,S五边形EDCMN=S四边形EFMN.
方案设计及理由得2分,作图得2分。
24、
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com