
题目列表(包括答案和解析)
4.9的相反数的倒数是( )
A.-9 B.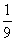 C.9
D.-
C.9
D.-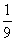
3.(2006年芜湖市)三峡工程是世界防洪效益最为显著的水利工程,它能有效控制长江上游洪水,增强长江中下游抗洪能力,据相关报道三峡水库的防洪库容22150000000m3,用科学计数法可记作( )
 A.221.5×108m3 B.22.15×109m3
A.221.5×108m3 B.22.15×109m3
C.2.215×1010m3 D.2215×107m3
2.(2005年长沙市)已知a、b两数在数轴上对应的点如图所示,下列结论正确的是( )
A.a>b B.ab<0 C.b-a>0 D.a+b>0

1.下列语句:①无理数的相反数是无理数;②一个数的绝对值一定是非负数;③有理数比无理数小;④无限小数不一定是无理数,其中正确的是( )
A.①②③ B.②③④ C.①②④ D.②④
17.(6分)解方程:(x+8)(x+1)= -12
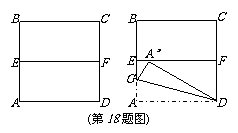 18.(8分)如图①,ABCD是一张正方形纸片,E、F分别为AB、CD的中点,沿过点D的折痕将A角翻折,使得点A落在EF上的A’处(如图②),折痕交AE于点G,那么∠ADG等于多少度?(写出计算步骤)
18.(8分)如图①,ABCD是一张正方形纸片,E、F分别为AB、CD的中点,沿过点D的折痕将A角翻折,使得点A落在EF上的A’处(如图②),折痕交AE于点G,那么∠ADG等于多少度?(写出计算步骤)
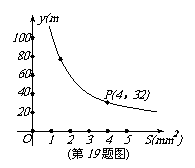 19.(8分)你吃过拉面?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示。
19.(8分)你吃过拉面?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示。
(1)写出y与s的函数关系式;
(2)求当面条粗1.6mm2时,面条的总长度是多少米?
 20.(9分)如图所示,要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙,墙长为a米,另三边用竹篱笆围成,已知篱笆总长为35m。
20.(9分)如图所示,要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙,墙长为a米,另三边用竹篱笆围成,已知篱笆总长为35m。
(1)求鸡场的长与宽各为多少米?
(2)题中的墙长度a米对题中的解起着怎样的作用?
 21.(9分)如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C’处,折痕DE交BC于点E,连结C’E,试判断四边形CDC’E是什么特殊四边形,并说明理由。
21.(9分)如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C’处,折痕DE交BC于点E,连结C’E,试判断四边形CDC’E是什么特殊四边形,并说明理由。
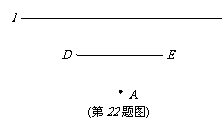 22.(10分)如图所示,小华家(点A处)和公路l之间竖着一块35米长且平行于公路的巨型广告牌(DE),广告牌挡住了小华的视线。请在图中画出视点A的盲区。并将盲区的那段公路记为BC,一辆以60千米/时匀速行驶的汽车经过公路BC段的时间是3秒。已知广告牌和公路的距离是40千米,求小华家到公路的距离(精确到1米)。
22.(10分)如图所示,小华家(点A处)和公路l之间竖着一块35米长且平行于公路的巨型广告牌(DE),广告牌挡住了小华的视线。请在图中画出视点A的盲区。并将盲区的那段公路记为BC,一辆以60千米/时匀速行驶的汽车经过公路BC段的时间是3秒。已知广告牌和公路的距离是40千米,求小华家到公路的距离(精确到1米)。
23.(10分)两人去某风景区游玩,每天某一时段开往该风景区有三辆汽车(票价相同),但是他们两人不知道这些车的车况好坏,也不知道汽车开过来的顺序,两人采取了不同的乘车方案:甲无论如何总是上开来的第一辆车,而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆车的舒适程度比第一辆好,他就上第二辆;如果第二辆车不比第一辆好,他就上第三辆车。若将这三辆车的舒适程度分为上、中、下三等,请你尝试解决如下问题:
(1)三辆车按出现的顺序共有哪几种不同的可能?请一一列举出来。
(2)你认为甲、乙两人采用的乘车方案中,哪一人采用的乘车方案使自己乘上等车的可能性大?为什么?
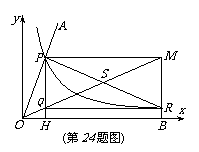
24.(12分)“三等分角”是数学史上一个著名的问题,但仅用尺规不可能三等分角,下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于平面直角坐标系中,边OB在x轴上,边OA与函数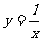 的图象交于点P,以P点为圆心,OP的2倍长为半径作弧交图象于点R,分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连结OM,则∠MOB=
的图象交于点P,以P点为圆心,OP的2倍长为半径作弧交图象于点R,分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连结OM,则∠MOB=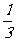 ∠AOB,要明白帕普斯的方法,请解决以下问题:
∠AOB,要明白帕普斯的方法,请解决以下问题:
(1)设P(a,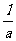 )、R(b,
)、R(b,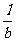 ),求直线OM对应的函数表达式(用含a、b的代数式表示);
),求直线OM对应的函数表达式(用含a、b的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q,请说明Q点在直线OM上,并以此为据证明∠MOB=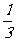 ∠AOB;
∠AOB;
(3)应用上述方法得到的结论,你认为如何三等分一个钝角?试用文字语言简要说明。
说明
在此,首先对潜江市园林二中陈老师表示感谢,谢谢陈老师提供了试卷。由于本人水平有限,编辑过程中难免出错,如有错落,请大家见谅。
天门市卢家口中学 Herewave
2007-2-7
09.已知一元二次方程有一根为2,那么这个方程可以是 (填上一个你认为正确的方程即可)。
10.如图,在△ABC中,AB=AC,BD、CE是△ABC的角平分线,写出除AB=AC以外的三组相等线段,它们是 。
11.已知反比例函数y=(2k-1)x 的图象上有两点P(x1,y1)、Q(x2,y2),且当x1<x2<0时,y1>y2,则其函数解析式为
。
的图象上有两点P(x1,y1)、Q(x2,y2),且当x1<x2<0时,y1>y2,则其函数解析式为
。
12.不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有3个,黄球1个,现从中任意摸出一个球是白球的概率是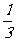 ,那么袋中蓝球有
个。
,那么袋中蓝球有
个。
13.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影可能是 (填序号)。

 14.如图,将圆筒中的水导入一个直径为40cm,高为55cm的圆容器中,圆桶放置的角度与水平线的夹角为45°,若使容器中的水面与圆桶相接触,则容器中水的深度至少应为
cm。
14.如图,将圆筒中的水导入一个直径为40cm,高为55cm的圆容器中,圆桶放置的角度与水平线的夹角为45°,若使容器中的水面与圆桶相接触,则容器中水的深度至少应为
cm。


15.如图,△OAP、△ABQ均为等腰直角三角形,点P、Q在函数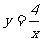 (x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标是
。
(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标是
。
16.用如图①的小菱形去拼一个大菱形,拼出的大菱形的较长对角线为88cm(如图②所示),则需要小菱形的个数是 。
在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号填入上面选择题答题表中相应题号下的方格内,填错或不填均为零分。
01.关于x的方程ax2+bx+c=0是一元二次方程的条件是( )。
A、a、b、c为任意实数 B、a、b不同时为零
C、a取不为零的实数 D、a取大于零的实数
02.下列说法正确的是( )。
A、等腰梯形既是中心对称图形,又是轴对称图形
B、矩形是轴对称图形,有四条对称轴
C、等腰三角形一腰上的高与底边的夹角等于顶角的一半
D、有一个角的平分线平分对边的三角形是等腰直角三角形
 03.某电视台举行歌手大奖赛,每场比赛都有编号为1-10号共10道综合素质测试题供选手随机抽取作答。在某场比赛中,前两位选手分别抽走了2号、7号题(抽走的题不再放回),则第3位选手抽中8号题的概率是( )。
03.某电视台举行歌手大奖赛,每场比赛都有编号为1-10号共10道综合素质测试题供选手随机抽取作答。在某场比赛中,前两位选手分别抽走了2号、7号题(抽走的题不再放回),则第3位选手抽中8号题的概率是( )。
A、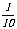 B、
B、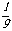 C、
C、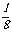 D、
D、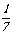
04.某工厂计划经过两年的时间将某种产品的产量从每年144万台提高到169万台,则每年平均约增长( )。
A、5% B、8% C、10% D、15%
05.如图,在△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数是( )。
A、15° B、30° C、50° D、65°
 06.如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则□ABCD的周长是( )。
06.如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则□ABCD的周长是( )。
A、24 B、18 C、16 D、12
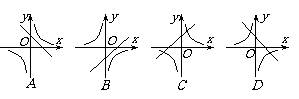 07.在同一直角坐标系中,函数y=kx-k与
07.在同一直角坐标系中,函数y=kx-k与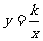 (k≠0)的图象大致是( )。
(k≠0)的图象大致是( )。

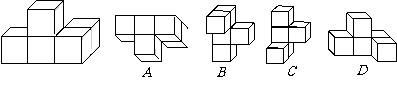 08.对于左边的几何体变换位置或视角,则可以得到的几何体是( )。
08.对于左边的几何体变换位置或视角,则可以得到的几何体是( )。
21. 解答(15分)
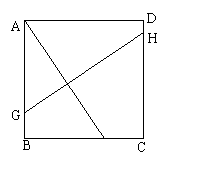 在正方形ABCD中,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10㎝,求GH的长。
在正方形ABCD中,M是BC上一点,连接AM,作AM的垂直平分线GH交AB于点G,交CD于点H,已知AM=10㎝,求GH的长。
20. 解答(12分)
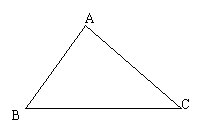
已知ABC,试设计一种变换,得到另一个三角形,使得这两个三角形能够拼成一个以AB、BC为一组邻边的平行四边形。
19. 四边形ABCD为正方形,△ADE经旋转后与△ABF重合,试问:
(1)旋转中心为哪个点?
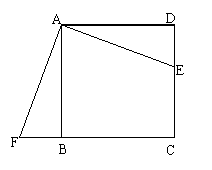 (2)旋转角是哪个角?度数是几度?
(2)旋转角是哪个角?度数是几度?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com