
题目列表(包括答案和解析)
1、某电视机厂计划用两年的时间把某种型号的电视机的成本降低36%, 若每年下降的百分数相同,则这个百分数为 ( )
A、10% B、20% C、120% D、180%
6、已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)如图1,AB为直径,要使得EF是⊙O的切线,只需保证∠CAE=∠_____,并证明之;
(2)如图2,AB为⊙O非直径的弦,(1)中你所添出的条件仍成立的话,EF还是⊙O的切线吗?若是,写出证明过程;若不是,请说明理由并与同学交流.
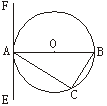
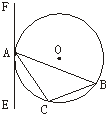
5、AB为⊙O的直径,把AB分成几条相等的线段.
以每条线段为直径画小圆,设AB=a,那么⊙O的周长为L=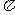 a,计算:
a,计算:
(1)把AB分成两条相等的线段,每个小圆的周长L2=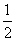
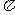 a=
a=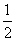 L.
L.
(2)把AB分成三条相等的线段,每个小圆的周长L3=________.
(3)把AB分成四条相等的线段,每个小圆的周长L4=________.
……
(4)把AB分成n条相等的线段,每个小圆的周长Ln=_______.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的_______.
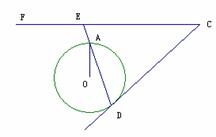
4、如图1所示,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连结AD交OC于点E,求证:CD=CE;
(2)若将图中的半径OB所在直线向上平行移动交OA于点F,交⊙O于点B′。其它条件不变(如图2所示),那么上述结论CD=CE还成立吗?为什么?
(3)若将图1中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其它条件不变(如图3所示),那么上述结论CD=CE还成立吗?(只写结论,不要证明)
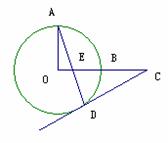 (图1)
(图1)
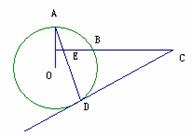 (图2)
(图2)
 (图3)
(图3)
(①证明:连接OD
∵CD是⊙O的切线, ∴∠CDO=90°
∵OA⊥OB ∴∠AOE=90°
∴∠AEO+∠A=90°
又∵OA=OD∴∠A=∠ODA
∴∠CDE=∠AEO 又∠AEO=∠CED ∴∠CDE=∠CED ∴CD=CE
②CE=CD仍然成立。
连接OD
∵原来的半径OB所在直线向上平行移动。∴CF⊥AO于F。
∴∠AFE=90°∴∠A+∠AEF=90°
∵CD是⊙O的切线∴∠ODC=90°∴∠ODE+∠CDE=90°
∵OA=OD∴∠A=∠ODE∴∠AEF=∠CDE
又∵∠AEF=∠CED ∴∠CED=∠CDE ∴CD=CE
③CE=CD仍然成立。)
3、如图,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合)。点Q在半圆O上运动,且总保持PQ=OP,过点Q作半圆O的切线交BA的延长线于点C。
⑴∠QPA=60°时,请你对△QCP的形状做出猜想,并证明你的结论;
⑵当QP⊥AB时,△QCP是 三角形;
 ⑶由⑴、⑵得出结论,请进一步猜想当点P在线段AM上运动到任何位置时,△QCP一定是 三角形。
⑶由⑴、⑵得出结论,请进一步猜想当点P在线段AM上运动到任何位置时,△QCP一定是 三角形。
3.若OA所在的直线向上平移且与⊙O无公共点,请你根
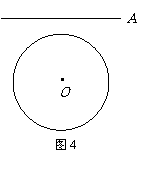 据原题中的条件完成图4,并判断结论是否还成立?
据原题中的条件完成图4,并判断结论是否还成立?
(只需交待判断)
(变化一、连接OQ,证明OQ⊥QR;
变化二 (1)、结论成立 (2)结论成立,连接OQ,证明∠B=∠OQB,则∠P=∠PQR,所以RQ=PR (3)结论仍然成立)
2.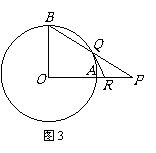 如图3,如果P在OA的延长线上时,BP交⊙O于Q,
如图3,如果P在OA的延长线上时,BP交⊙O于Q,
过点Q作⊙O的切线交OA的延长线于R,原题中的结论
还成立吗?为什么?
1.如图2,若OA向上平移,变化一中的结论还成立吗?(只需交待判断) 答: .
2、有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.说明:RP=RQ.
请探究下列变化:
变化一:交换题设与结论.
已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ. .
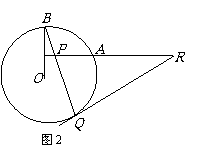
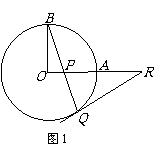 说明:RQ为⊙O的切线. .
说明:RQ为⊙O的切线. .
变化二:运动探求.
1、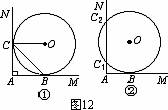 如图12①,直线AM⊥AN, ⊙O分别与AM、AN相切于B、C两点,连结OC、BC,则有∠ACB=∠OCB;(请思考:为什么?)若将图12①中直线AN向右平移,与⊙O相交于C1、C2两 点,⊙O与AM的切点仍记为B,如图12②.
如图12①,直线AM⊥AN, ⊙O分别与AM、AN相切于B、C两点,连结OC、BC,则有∠ACB=∠OCB;(请思考:为什么?)若将图12①中直线AN向右平移,与⊙O相交于C1、C2两 点,⊙O与AM的切点仍记为B,如图12②.
(1)请你写出与平移前相应的结论,并将图12②补充完整;
(2)判断此结论是否成立,并说明理由.
((1)图②中相应结论为∠AC1B=∠OC1B和∠AC2B=∠OC2B.(2)以前者为例进行证明:连接OB、OC1,∵AM与⊙O相切于B,∴OB⊥AM.∵AN⊥AM,∴OB∥AN.∴∠AC1B=∠OBC1. ∵OB=OC1,∴∠OBC1=∠OC1B.故∠AC1B=∠OC1B.同理可证∠AC2B=∠OC2B.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com