8、如图，已知：梯形ABCD中，AD//BC，EF过O点且平行于BC，求证：EO=FO。

7、如图，点D、E分别在AC、BC上，如果测得CD＝20m，CE＝40m，AD=100m，BE=20m，DE=45m,求A、B两地间的距离。

6、小明的身高是1.7米，他的影子长是2米，同一时刻学校旗杆的影子长是20米，求旗杆的高。

5、如图，A、B两点被池塘隔开，在AB外任选一点C，连结AC、BC分别取其三等分点M、N量得 MN＝38m。求AB的长。

4、如图，A为河对岸一点，AB⊥BC，DC⊥BC，垂足分别为B、C，直线AD、BC相交于点E,如果测得BF＝80m，CE=40m，CD=30m，求河宽AB

3、如图，零件的外径为16cm，要求它的壁厚x，需要先求出内径AB，现用一个交叉钳(AD与BC相等)去量，若测得OA:OD=OB:OC=3:1，CD＝5cm，你能求零件的壁厚x吗？

2、已知：如图1，AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证明成立(不要求考生证明).若将图1中的垂线改为斜交，如图2，AB∥CD，AD，BC相交于点E，过点E作EF∥AB，交BD于点F，则：

⑴　　 还成立吗？如果成立，请给出证明；

如果不成立，请说明理由；

⑵　　　 请找出S_△ABD，S_△BED和S_△BDC间的关系式，并给出证明.

1、(06浙江台州)善于学习的小敏查资料知道：对应角相等，对应边成比例的两

个梯形，叫做相似梯形.他想到“平行于三角形一边的直线和其

他两边相交，所构成的三角形与原三角形相似”，提出如下两个

问题，你能帮助解决吗？

问题一　 平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似？

(1)从特殊情形入手探究.假设梯形ABCD中， AD∥BC，AB=6，BC=8，CD=4，

AD=2，MN是中位线(如图①).根据相似梯形的定义，请你说明梯形AMND与梯形ABCD是否相似?

(2)一般结论：平行于梯形底边的直线截两腰所得的梯形与原梯形______________　　　　　　　 (填“相似”或“不相似”或“相似性无法确定”.不要求证明) .

问题二　 平行于梯形底边的直线截两腰所得的两个小梯形是否相似?

(1)从特殊平行线入手探究.梯形的中位线截两腰所得的两个小梯形______________　　　　　　　 (填“相似”或“不相似”或“相似性无法确定”.不要求证明).

(2)从特殊梯形入手探究.同上假设，梯形ABCD中，AD∥BC，AB=6，BC=8，CD=4，AD=2，你能找到与梯形底边平行的直线PQ(点P,Q在梯形的两腰上，如图②), 使得梯形APQD与梯形PBCQ相似吗? 请根据相似梯形的定义说明理由.

(3)一般结论：对于任意梯形(如图③)，一定　　　　 (填“存在”或“不存在”)

平行于梯形底边的直线PQ，使截得的两个小梯形相似.

若存在，则确定这条平行线位置的条件是=　 　　　

(不妨设AD= a，BC= b，AB=c，CD= d.不要求证明 ) .

8、(06深圳)如图，抛物线与轴交于、两点(点在点的左侧)，抛物线上另有一点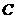在第一象限，满足∠为直角,且恰使△∽△.

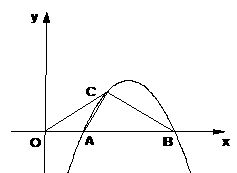(1)求线段的长.

(2)求该抛物线的函数关系式．

(3)在轴上是否存在点，使△为等腰三角形？若存在，求出所有符合条件的点的坐标；若不存在，请说明理由.

　 解：

练习：

7、如图①，梯形ABCD中，AD∥BC，E、F分别在AB、CD上，且EF∥BC，EF分别交BD、AC于M、N。(1)求证：ME=NF；(2)当EF向上平移至②③④各个位置时，其他条件不变，(1)的结论是否还成立？请分别证明你的判断。