
题目列表(包括答案和解析)
3.如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为圆心 ,正方形的对角线长为半径画弧,交数轴于点A,点A表示数x,则x2的平方根是 ( )
 (A)
(A)  (B)
(B)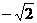
(C)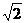 (D)2
(D)2
2.在平面直角坐标系中,点A( ,
, )在第四象限,那么点
)在第四象限,那么点
B( ,
, )在
( )
)在
( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
1.如果 ,那么代数式m是
( )
,那么代数式m是
( )
(A) (B)
(B) (C)
(C) (D)
(D)
7、 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达B、C),连结AD,作∠ADE=45°,交AC于E,①找出图中的相似三角形,并证明,②设BD=x,AE=y,求y与x的函数关系式,并写出自变量x的取值范围;③当x为何值时,△ADE是以AE为底的等腰三角形。
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达B、C),连结AD,作∠ADE=45°,交AC于E,①找出图中的相似三角形,并证明,②设BD=x,AE=y,求y与x的函数关系式,并写出自变量x的取值范围;③当x为何值时,△ADE是以AE为底的等腰三角形。
6、 (8分)在直角坐标系内,过点C(3,6)分别作x轴和y轴的垂线CB和CA,垂足分别为B和A,若点P从点O沿OB向B以1个长度单位/秒的速度运动,点Q从点B沿BC向C以2个长度单位/秒的速度运动,如果P、Q分别从O、B同时出发。试求:
(8分)在直角坐标系内,过点C(3,6)分别作x轴和y轴的垂线CB和CA,垂足分别为B和A,若点P从点O沿OB向B以1个长度单位/秒的速度运动,点Q从点B沿BC向C以2个长度单位/秒的速度运动,如果P、Q分别从O、B同时出发。试求:
① 经过多少时间,△PBQ的面积等于2个平方单位;
② 线段PQ与AB能否垂直?若能垂直,求出此时点Q的坐标;若不能,则说明理由。
5、 (8分)已知:A(-1,0),B(4,O),点C在y轴上,且∠ACB=90°
(8分)已知:A(-1,0),B(4,O),点C在y轴上,且∠ACB=90°
⑴求点C的坐标; ⑵求经过A、B、C三点的抛物线的解析式
4、 (8分)某市经济开发区建有
(8分)某市经济开发区建有
 三个食品加工厂,这三个工厂和开发区
三个食品加工厂,这三个工厂和开发区 处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且
处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且 米,
米, 米.自来水公司已经修好一条自来水主管道
米.自来水公司已经修好一条自来水主管道 两厂之间的公路与自来水管道交于
两厂之间的公路与自来水管道交于 处,
处,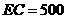 米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
(1)要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?并在图形中画出;
(2)求出各厂所修建的自来水管道的最低的造价各是多少元?
3、 (8分)小明发现电线杆AB的影子落在土坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,请你计算电线杆的高度为多少?
(8分)小明发现电线杆AB的影子落在土坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,请你计算电线杆的高度为多少?
2、 (8分)已知:矩形ABCD,AB=2BC,请在图①,图②中分别画两条线段,把矩形分割成互相相似的三个三角形,要求:
(8分)已知:矩形ABCD,AB=2BC,请在图①,图②中分别画两条线段,把矩形分割成互相相似的三个三角形,要求:
(1)画出两种不同的方法;(2)标上必要的字母,指明相互相似的三角形(工具不限,不要求写画法和证明过程)
1、 (8分)如图,正方形ABCD的边长是2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,求当CM为多少时,△AED与N、M、C为顶点的三角形相似。
(8分)如图,正方形ABCD的边长是2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,求当CM为多少时,△AED与N、M、C为顶点的三角形相似。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com