15.3　 点拨:x²-3x-1=0的△=13>0,x²-x+3=0的△=-11<0所有实根和,就是方程x²-3x-1=0中两根之和,由根与系数的关系求得两根之和等于3.

14.3　 点拨:设两根为x₁,x₂,根据根与系数的关系x₁+x₂=4, x₁·x₂=,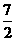

由勾股定理斜边长的平方=(x₁+x₂)²-2x₁x₂=16-2×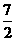=9,∴斜边长为3.

13.a+b+c=0,b=a+c,c=0.

12.a=1,b=-2. 点拨:-1是两方程的根,则3a+b-1=0,a-2b-5=0,解得a=1,b=-2.

11.m=-6,另一根为3+.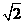

点拨:根据一元二次方程根与系数的关系, 设方程另一个根为x₁ ,

则(3-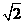)x₁=7,x₁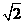=3+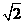,(3+)+(3-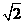)=-m,则m=-6.

10.D　 点拨:两方程有相同实根,则x²+k²-16=x²-3k+12,解得k=-7或4,

当k=- 7时,方程无实根,∴k=4.

9.A　 点拨:∵x²≥0,│x│≥0,∴x²-4│x│+3=0的解就是方程│x│²-4│x│+3=0的解,(│x│-3)(│x│-1)=0,x=±3或x=±1.

8.A　 点拨:使分式的值为零的条件:分子=0分母≠0,x²-5x-6=0,x=6或-1,x+ 1≠0,x≠-1,故x=6,本题易漏分母不能为零这个条件.

7.D. 点拨:设x²-kx+b=0的两根为x₁,x₂,则x²+kx+6=0的两根为x₁+5,x₂+5,因为x₁+x₂=k, (x₁+5)+(x₂+5)=-k所以k=-5.

6.D.　 点拨:方程有两个实数根,所以△≥0,即[2(k+2)]²-4k²≥0,解得k≥-1, 两实数根之和大于-4,即-2(k+2)>-4,k<0,

∴-1≤k<0.本题易忽略有两实根, 需满足△≥0这个重要条件.