
题目列表(包括答案和解析)
7.(江西省)某公司2003年缴税60万元,2005年缴税80万元,设该公司这两年缴税的年平均增长率为x,则得到方程( )
A、60+2x=80 B、60(x+1)=80 C、60x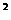 =80 D、60(x+1)
=80 D、60(x+1)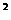 =80
=80
6.(江西省)已知关于x的一元二次方程x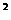 +kx-1=0 ,(1)求证:方程有两个不相等的实数根; (2)设方程的两根分别为x
+kx-1=0 ,(1)求证:方程有两个不相等的实数根; (2)设方程的两根分别为x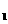 ,x
,x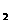 ,且满足x
,且满足x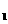 +x
+x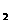 =x
=x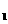 ·x
·x ,求k的值。
,求k的值。
5.(江西省)小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a>8),就站在A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍上,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人。
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少(用含a的代数式表示)?
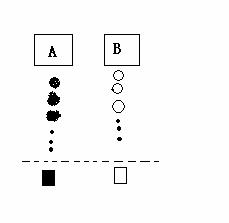 (2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围(不考虑其它因素)。
(2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围(不考虑其它因素)。
4.(2006年大连市)已知关于x的方程x2+kx-2=0的一个解与方程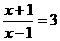 解相同。
解相同。
(1)求k的值;(2)求方程x2+kx-2=0的另一个解。
3.(2006年大连市)今年4月某天的最高气温为8℃,最低气温为2℃,则这天气温t℃的t的取值范围是________________。
2.(06年重庆市)不等式组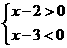 的解集是()A.
的解集是()A.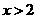 B.
B.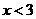 C.
C.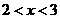 D.无解
D.无解
1.(2006年浙江省绍兴市)不等式2-x>1的解集是 A.z>1 B.x<1 C.z>-1 D.z<-1
26.(10分)已知:如图,⊙O与⊙P相交于A、B两点,点 P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点 E作EF⊥CE交CB的延长线于F。
(1)求证:BC是⊙P的切线;
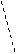
 (2)若CD=2,CB=
(2)若CD=2,CB=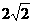 ,求EF的长;
,求EF的长;
(3)求以BP、EF为根的一元二次方程;
解:(1)∵点 P在⊙O上。连结PB,
∵CP为直径,∴∠CPB =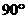 ,
,
∴PB⊥CB,∵B在⊙P上,
∴CB是⊙P的切线。
(2)∵CB是⊙P的切线,∴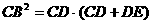 ,∵
,∵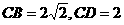 ,
,
∴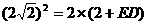 ,∴
,∴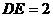 ,∴
,∴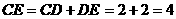 ,
,
∴在⊙P中,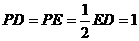 ,
,
在Rt⊿CPB中,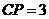 ,
,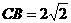 ,∴
,∴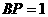 ,
,
∵EF⊥CE,∴∠FEC =∠CBP =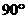 ,∠FCE =∠PCB,∴⊿FCE∽⊿PCB,
,∠FCE =∠PCB,∴⊿FCE∽⊿PCB,
∴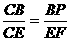 ,而
,而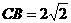 ,
,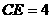 ,
,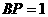 ,∴
,∴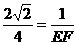 ,∴
,∴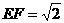
(3)∵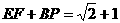 ,
,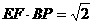
∴所求以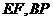 为根的方程是:
为根的方程是: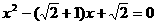
25. (10分)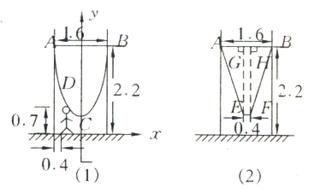 为供孩子们打秋千,把绳子剪断后,中间系上一块长为
为供孩子们打秋千,把绳子剪断后,中间系上一块长为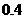 米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,(1)求绳子未剪断时最低点到地面的距离;(2)求剪断绳子系上木板时,木板到地面的距离。(供选用数据:
米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,(1)求绳子未剪断时最低点到地面的距离;(2)求剪断绳子系上木板时,木板到地面的距离。(供选用数据: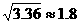 ,
,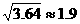 ,
,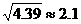 )
)
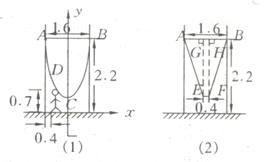
解:(1)如图,建立直角坐标系,
设二次函数为: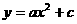
∵D(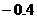 ,
,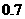 ),
),
B(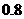 ,
,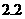 )
)
∴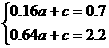
 ∴
∴ ,∴绳子最低点到地面的距离为
,∴绳子最低点到地面的距离为
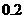 米。
米。
(2)分别作EG⊥AB于G,EH⊥AB于H,
AG =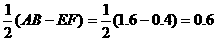
在Rt⊿AGE中,
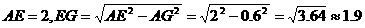
∴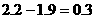 (米)
(米)
∴木板到地面的距离约为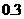 米。
米。
24.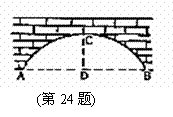 (10分)有一个拱桥是圆弧形,他的跨度为60
(10分)有一个拱桥是圆弧形,他的跨度为60 ,拱高为18
,拱高为18 ,当洪水泛滥跨度小于30
,当洪水泛滥跨度小于30 时,要采取紧急措施。若拱顶离水面只有4
时,要采取紧急措施。若拱顶离水面只有4 时,问是否要采取紧急措施?
解:作出圆弧形的圆心O,
时,问是否要采取紧急措施?
解:作出圆弧形的圆心O,
在Rt⊿OAD中,
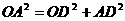 ,而OA =
,而OA = ,AD = 30,CD = 18
,AD = 30,CD = 18
∴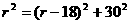
∴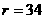
当拱顶里水面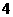 米时,水面所在弦的弦心距为:
米时,水面所在弦的弦心距为:
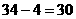 米,设水面所在的弦为
米,设水面所在的弦为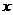 ,由勾股定理可知:
,由勾股定理可知:
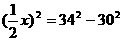 ,∴
,∴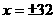 ,负值舍去,∴
,负值舍去,∴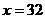
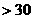
∴不用采取紧急措施。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com