
题目列表(包括答案和解析)
9、 (8分)如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处.测得仰角为60°.那么该塔有多高?(小明的身高忽略不计,结果精确到1 m)
(8分)如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处.测得仰角为60°.那么该塔有多高?(小明的身高忽略不计,结果精确到1 m)
8、(8分)如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是45o ,而大厦底部的俯角是37o ,求该大厦的的高度(结果精确到0.1m).
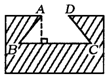
7、(8分)如图所示的燕尾槽一个等腰梯形,外口AD宽10cm,燕尾槽深10cm,AB的坡度i=1:1,求里口宽BC及燕尾槽的截面积.

6、
 (8分)如图:某同学用一个有60°角的直角三角板估测学校旗杆AB的高度,他将60°角的直角边水平放在1.5米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5米,则旗杆AB的高度约为多少米。(精确到1米,
(8分)如图:某同学用一个有60°角的直角三角板估测学校旗杆AB的高度,他将60°角的直角边水平放在1.5米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5米,则旗杆AB的高度约为多少米。(精确到1米, 取1.732)
取1.732)
5、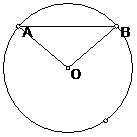 (10分) 已知:如图,在⊙O中,
(10分) 已知:如图,在⊙O中, 长为4cm,OA=3cm..求:
长为4cm,OA=3cm..求:
(1)∠AOB度数(精确到1度)
(2)AB的长度(精确到0.1)
(3)
4、(16分)根据下列条件解直角三角形.(Rt△ABC中,∠C=900)
①  ②
②  =
= (边长保留3个有效数字,度数取整)
(边长保留3个有效数字,度数取整)
3、(8分)计算:(1)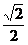 sin45°+sin60°-2cos45°
sin45°+sin60°-2cos45°
(2)sin230°+cos245°+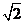 sin60°·tan45°;
sin60°·tan45°;
2、选择:(18分)
(1)在Rt△ABC中,如果一条直角边和斜边的长度都缩小至原来的 ,那么锐角A的各个三角函数值( )
,那么锐角A的各个三角函数值( )
A.都缩小 B.都不变 C.都扩大5倍 D.无法确定
B.都不变 C.都扩大5倍 D.无法确定
(2)已知Rt△ABC中,∠C=90°,tanA= ,BC=8,则AC等于( )
,BC=8,则AC等于( )
A.6 B. C.10 D.12
C.10 D.12
(3)已知∠A是锐角,且sinA= ,那么∠A等于( )
,那么∠A等于( )
A.30° B.45° C.60° D.75°
(4)在Rt△ABC中,∠C=90°,已知α和A,则下列关系式中正确的是( )
(A)c=a·sinA(B)c= (C)c=a·cosA(D)c=
(C)c=a·cosA(D)c=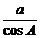
(5)某水库大坝的横断面是梯形,坝内斜坡的坡度 ,坝外斜坡的坡度
,坝外斜坡的坡度 ,则两个坡角的和为
( )
,则两个坡角的和为
( )
A、 B、
B、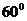 C、
C、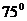 D、
D、
(6)在△ABC中,A,B为锐角,且有
 ,则这个三角形是 ( )
,则这个三角形是 ( )
A、等腰三角形 B、直角三角形 C、钝角三角形 D、锐角三角形
1、 填空:(16分)
(1) 三角函数的定义:sinA= cosA=
tanA=
(2)在△ABC中,∠C=90°, ,则cosB=___________.
,则cosB=___________.
(3)Rt△ABC中,∠C=90°, ,则∠B=_________度.
,则∠B=_________度.
(4)△ABC中,∠C=90°, ,则AC=_________.
,则AC=_________.
(5)已知△ABC中,AB= ,∠B=450,∠C=600,AH⊥BC于H,则AH= ;
,∠B=450,∠C=600,AH⊥BC于H,则AH= ;
CH= .
26. (12分)在探讨圆周角与圆心角的大小关系时,小亮首先考虑了一种特殊情况(圆心在圆周角的一边上)如图(1)所示:
(12分)在探讨圆周角与圆心角的大小关系时,小亮首先考虑了一种特殊情况(圆心在圆周角的一边上)如图(1)所示:
∵∠AOC是⊿ABO的外角
∴∠AOC=∠ABO+∠BAO
又∵OA=OB
∴∠OAB=∠OBA ∴∠AOC=2∠ABO
即∠ABC= ∠AOC
∠AOC
如果∠ABC的两边都不经过圆心,如图(2)、(3),那么结论会怎样?请你说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com