8．已知半径为1的圆心在原点，半径为3的圆的圆心坐标是(-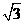，1)，则两圆位置关系是(　 )

　　 A．外切　　 B．内切　　 C．相交　　 D．外离

7．已知AB是两个同心圆中大圆的弦，也是小圆的切线，设AB=a，用a表示这两个同心圆中圆环的面积为(　 )

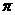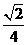
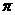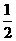
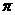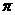　　 A．a²　　　 B．a²　　　 C．a² 　　D．a²

6．某校去年对实验器材的投资为2万元，预计今明两年的投资总额为8万元，若设该校这两年在实验器材投资上的平均增长率为x，则可列方程____　　　　　 __．

5．小明所在的年级共有10个班，每个班有45名学生，现从每个班中任抽一名学生共10名学生参加一次活动，小明被抽到的概率为(　 )

　　 A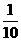．　　　 B．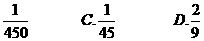

4．已知△ABC中，AB=AC，∠A=50°，⊙O是△ABC的外接圆，D是优弧BC上任一点(不与A、B、C重合)，则∠ADB的度数是(　 )

　　 A．50°　 B．65°　 C．65°或50°　　 D．115°或65°

3．用配方法将二次三项式a²+4a+5变形，结果是(　 )

　　 A．(a-2)²+1　　 B．(a+2)²+1　　 C．(a-2)²-1　 D．(a+2)²-1

2．若x>2，化简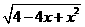的结果是(　 )

　　 A．x+2　　 B．±(x-2)　　 C．2-x　　 D．x-2

1．关于x的一元二次方程x²+kx－1=0的根的情况是

A、有两个不相等的同号实数根　　 B、有两个不相等的异号实数根

C、有两个相等的实数根　　 　　 D、没有实数根

30．已知抛物线y＝x²－kx+k+4与x轴正半轴从左到右交于点A(x₁，0)和B(x₂，0)不同的两点，与Y轴交于G，H为OG中点，且x₁²+x₂²＝40

(1)求此抛物线的解析式及顶点C坐标；

(2)若抛物线的对称轴交X轴于D，E为DC中点；过A、B、E三点作圆，过H的直线与该圆相切于P，求直线HP的方程；

(3)设F(m，n)为抛物线上一点，若解析式为y＝a的直线MN与抛物线交点为M、N，是否存在实数a，使得△MNF为等边三角形，若存在，求出a的值；若不存在，请说明理由。

(第30题)　　　　　　　　

29．如图：⊙O与直线PC相切于点C，直径AB∥PC，PA交⊙O于D，BP交⊙O于E，DE交PC于F

(1)求证：PF²＝EF·FD

(2)当tan∠APB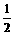＝，tan∠ABE＝，AP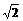＝时，求PF的长。

(3)在(2)条件下，连接BD，判断△ADB是什么三角形？并证明你的结论。

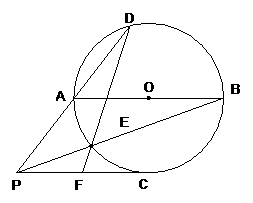
(第29题)