
题目列表(包括答案和解析)
19.(2006年泰州市)半径分别为6 和4
和4 的两圆内切,则它们的圆心距为
的两圆内切,则它们的圆心距为  .
.
18.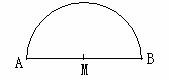 (2006年南安市)如图,半圆M的直径AB为20cm,现将半圆M绕着点A顺时针旋转180°.(1)请你画出旋转后半圆M的图形;(2)求出在整个旋转过程中,半圆M所扫过区域的面积(结果精确到1cm
(2006年南安市)如图,半圆M的直径AB为20cm,现将半圆M绕着点A顺时针旋转180°.(1)请你画出旋转后半圆M的图形;(2)求出在整个旋转过程中,半圆M所扫过区域的面积(结果精确到1cm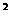 ).
).
⑴画图略 ;⑵ 半圆M所扫过的面积=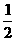 ×∏×20
×∏×20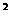 +
+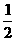 ×∏×10
×∏×10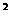 =250∏≈758(cm
=250∏≈758(cm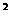 )。
)。
17.(06年江西省南昌市)两圆半径分别为5和3,圆心距为8,则两圆的位置关系是[ ]C
A内切 B相交 C外切 D外离
16.(2006年江西省南昌市)如图AB是⊙O的直径,BC是⊙O弦OD⊥CB于点E,交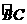 于点D
于点D
(1)请写出三个不同类型的正确结论:
(2)连结CD,设∠CDB=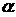 ,∠ABC=
,∠ABC=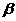 ,试找出
,试找出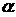 与
与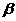 之间的一种关系式并给予证明.
之间的一种关系式并给予证明.
(1)不同类型的正确结论不惟一.以下答案供参考:
①BE=CE 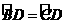 ②,③∠BED=90°④∠BOD=∠A,
⑤AC∥OD
②,③∠BED=90°④∠BOD=∠A,
⑤AC∥OD
⑥AC⊥BC ⑦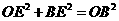 ⑧
⑧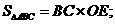 ⑨ΔBOD是等腰三角形⑩ΔBOE∽ΔBAC等,
⑨ΔBOD是等腰三角形⑩ΔBOE∽ΔBAC等,
(2) 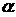 与
与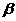 的关系式主要有如下两种形式,请参照评分:
的关系式主要有如下两种形式,请参照评分:
①答;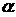 与
与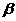 之间的关系式为
之间的关系式为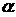 -
-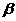 =90°
=90°
证明:∵AB为⊙O的直径,∴∠A+∠ABC=90°,又∵四边形ACDB为圆的内接四边形,∴∠A+∠CDB=180°∴∠CDB-∠ABC=90°,即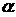 -
-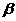 = 90°。 说明:关系式写成
= 90°。 说明:关系式写成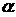 = 90°+
= 90°+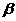 或
或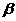 =
=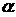 -90°均参照给分
-90°均参照给分
②答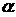 与
与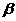 之间的关系式为;
之间的关系式为;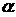 >2
>2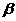
证明 ∵ OD=OB , ∴∠ODB=∠ OBD,又∵∠ OBD=∠ABC+∠CBD ∴∠ODB>∠ABC
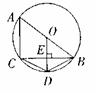 ∵OD⊥BC
∴
∵OD⊥BC
∴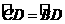 ∴CD=BD,∴∠CDO=∠ODB=
∴CD=BD,∴∠CDO=∠ODB=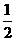 ∠CDB,∴
∠CDB,∴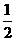 ∠CDB>∠ABC,
∠CDB>∠ABC,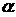 >2
>2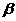 。说明:若得 出与
。说明:若得 出与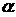 与
与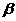 的关系式为
的关系式为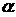 >
>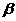 ,且证明正确的也给满分
,且证明正确的也给满分
15.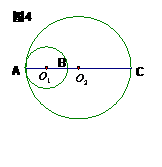 (2006年贵阳市)如她4,B是线段AC上的一点,且
(2006年贵阳市)如她4,B是线段AC上的一点,且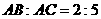 ,分别以AB、AC为直径画圆,则小圆的面积与大圆的面积之比为
;4:25
,分别以AB、AC为直径画圆,则小圆的面积与大圆的面积之比为
;4:25
14.(2006年贵阳市)如图3,⊙O是等边三角形ABC的外接圆,点D是⊙O上一点,则∠BDC = ;60
13.(2006年旅顺口区)如图,AB与⊙O切于点B,AO=6㎝,AB=4㎝,则⊙O的半径为 ( ) B
 A、4
A、4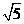 ㎝ B、2
㎝ B、2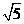 ㎝ C、2
㎝ C、2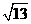 ㎝ D、
㎝ D、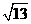 ㎝
㎝
12. (2006年旅顺口区)如图,点D在以AC为直径的⊙O上,如果∠BDC=20°,那么∠ACB= . 70°;
(2006年旅顺口区)如图,点D在以AC为直径的⊙O上,如果∠BDC=20°,那么∠ACB= . 70°;
11.(2006年旅顺口区)若圆锥的底面周长为20π,侧面展开后所得扇形的圆心角为120°,则圆锥的侧面积为 .300π;
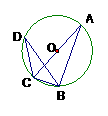
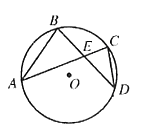
10.(2006年海淀区)如图,在⊙O中,弦AC与BD交于E, ,求CD的长。
,求CD的长。
 解:
解:
解:因为弦AC与BD交于E,所以A、B、C、D是⊙O上的点
所以∠B=∠C,∠A=∠D, 所以△ABE∽△DCE, 所以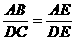 ,
,
所以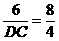 ,所以
,所以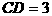 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com