
题目列表(包括答案和解析)
4、AB是⊙O的直径,弦CD⊥AB于P(P在OB上),CD=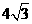 ,OP=2,则AC的长是( )
,OP=2,则AC的长是( )
A、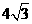 B、
B、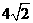 C、
C、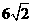 D、
D、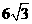
3、圆的弦与直径相交成30°角,并且分直径为8㎝和2㎝两部分,则弦心距等于 ㎝。
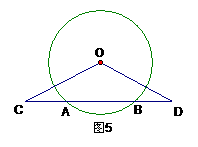
2、如图6,DE是⊙O的直径,弦AB⊥DE,垂足为C,若AB=6,CE=1,则CD= ,OC= 。

1、在直径为20㎝的圆中,弦心距是6㎝的弦长是 ㎝。
5、 在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦心距中,有一组量相等,那么它们所对应的其余各组量都 。
典型考题
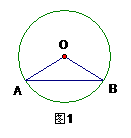
例1、如图1,在⊙O中,圆心角∠AOB=120°,弦AB=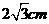 ,则⊙O的半径是 。
,则⊙O的半径是 。
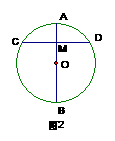
例2、如图2,已知AB为⊙O的直径,且AB⊥CD,垂足为M,CD=8,AM=2,则OM= 。
例3、⊙O的半径是5,P是圆内一点,且OP=3,则过点P的最长弦是 ,最短弦是 。
例4、如图3,AB是⊙O的直径,CD是弦,若AB=10㎝,CD=8㎝,那么A、B两点到直线CD的距离之和为( )㎝。
A、12 B、10 C、8 D、6
例5、如图4,在Rt△ABC中,∠C=90°,AC=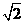 ,BC=1,若以C为圆心、CB的长为半径的圆交AB于P,则AP= 。
,BC=1,若以C为圆心、CB的长为半径的圆交AB于P,则AP= 。

同步训练
4、 垂径定理的条件是 ,结论是 。
3、 圆是以为 轴的轴对称图形,又是以 为中心的中心对称图形。
2、 的三点确定一个圆;任何一个三角形都有一个外接圆,外接圆的圆心叫做三角形的 心,它是三角形的 的交点。
1、 圆是平面上到 的距离等于 的点的集合。
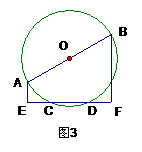
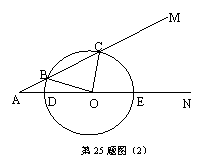
20.(2006年泰州市)已知:∠MAN=30°,O为边AN上一点,以O为圆心、2为半径作⊙O,交AN于D、E两点,设AD= ,
,
⑴如图⑴当 取何值时,⊙O与AM相切;
取何值时,⊙O与AM相切;
⑵如图⑵当 为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
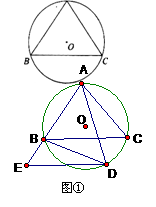
(2006年苏州市) 如图①,△ABC内接于⊙0,且∠ABC=∠C,点D在弧BC上运动.过点D作DE∥BC.DE交直线AB于点E,连结BD. (1)求证:∠ADB=∠E; (2)求证:AD2=AC·AE; (3)当点D运动到什么位置时,△DBE∽△ADE请你利用图②进行探索和证明
 A
A
A
A
证:∵DE∥BC,∴∠ABC=∠E,∵∠ADB, ∠C都是AB所对的圆周角,
∴∠ADB=∠C, 又∠ABC=∠C, ∴∠ADB=∠E
(2) ∵∠ADB=∠E,∠BAD=∠DAE. ∴△ADB∽△AED ∴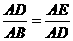 ,即AD2=AB·AE
,即AD2=AB·AE
∵∠ABC=∠C,∴AB=AC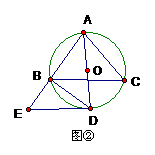 ∴AD2=AC·AE
∴AD2=AC·AE
(3)点D运动到弧BC中点时.△DBE∽△ADE, ∵DE∥BC.∴∠EDB=∠DBC.
∵∠DBC所对的是弧DC, ∠EAD所对的是弧DB, ∴∠DBC=∠EAD, ∴∠EDB=∠EAD
又∠DEB=∠AED, ∴△DBE∽△ADE
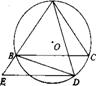
(06年连云港市)(本小题满分10分)如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC至点D,使CD=AC,连接AD交⊙O与点E,连接BE、CE与AC交于点F。
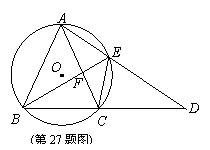 (1)求证:△ABE≌△CDE;
(1)求证:△ABE≌△CDE;
(2)若AE=6,DE=9,求EF的长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com