
题目列表(包括答案和解析)
9、用计算器求下列余弦值,并用“<”连接:(6分)
cos27.5°, cos85°, cos63°36’15”, cos54°23’, cos38°39’52”
你从这些能找到什么规律。
8、在 中,
中,  =90
=90 ,
,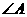 =30°,AB=4。求BC,AC的长。(6分)
=30°,AB=4。求BC,AC的长。(6分)
7、(6分)如图,身高1.5m的小丽用一个两锐角分别是30º和60º 的三角尺测量一棵树的高度.已知她与树之间的距离为5m,那么这棵树大约有多高?

6、计算:(4×4=16分)
(1)sin30º+cos45º; (2) sin²60º+cos²60º-tan45º.
(3)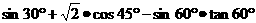
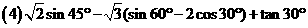
5、填下表:(9分)
|
三角函数 |
30º |
45º |
60º |
|
sin |
|
|
|
|
cos |
|
|
|
|
tan |
|
|
|
4、选择:(9分)(1)在Rt△ABC中,∠C=900,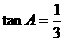 ,AC=6,则BC的长为( )
,AC=6,则BC的长为( )
A、6 B、5 C、4 D、2
(2)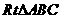 中,
中, =90
=90 ,
,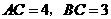 ,
,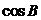 的值为 ( )
的值为 ( )
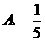
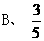
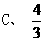
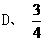
(3) 中,
中, =90
=90 ,
,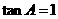 ,则
,则 的值是 (
)
的值是 (
)
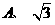
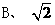
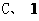
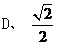
3、填空:(6分)(1)在Rt△ABC中,∠C=900,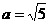 ,
,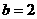 ,则sinA=
。
,则sinA=
。
(2)在Rt△ABC中,∠A=900,如果BC=10,sinB=0.6,那么AC= 。
(3)在 中,
中, =90
=90 ,c = 8 , sinA =
,c = 8 , sinA = 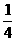 ,则
,则 = .
= .
2、在Rt△ABC中,∠C=900,AC=12,BC=15。(8分)
(1)求AB的长;
(2)求sinA、cosA的值;
(3)求 的值;
的值;
(4)比较sinA、cosB的大小。
1、用三角函数的定义求出∠A的正弦,余弦,正切。(8分)
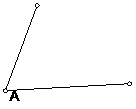
28、(14分)如图,已知过A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点。
(1)经过多少时间,线段PQ的长度为2?
(2)写出线段PQ长度的平方y与时间t之间的函数关系式和t的取值范围;
(3)٭在P、Q运动过程中,是否可能出现PQ⊥MN?若有可能,求出此时间t;若不可能,请说明理由;
(4)٭是否存在时间t,使P、Q、M构成的三角形与△MON相似?若存在,求出此时间t;若不可能,请说明理由;
 y
y
N A
Q




 O P M x
O P M x
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com