7、　 已知一个直角三角形斜边长6cm，则斜边上的中线长为__________ cm。

6、　 三角形的三条中位线围成的三角形的周长为10cm，则原三角形的周长是_______________cm。

5、　 已知：直角三角形ABC中，∠C=90°，斜边AB=24cm，∠A=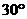，则直角边AC=_____________cm，斜边上的高是___________cm。

4、　 命题：“全等三角形的对应角相等”的逆命题是______________________________________。这条逆命题是______命题(填“真”或“假”)

3、　 等腰三角形的顶角为30°，腰长为16cm，则它腰上的高是__________cm，面积是_____________cm²。

2、　 已知△ABC中，∠A：∠B：∠C=1：2：3，则这个三角形的度数分别为______________________。

1、　 已知MN是线段AB的垂直平分线，P是MN上任意一点，则______=________。

20、(安徽省　 2003年)如图1-16，这些等腰三角形与正三角形的形状有差异，我们把它与正三角形的的接近程度称为“正度”。在研究“正度”时，应保证相似三角形的“正度”相等。设等腰三角形的底和腰分别为a、b，底角和顶角分别为α、β。要求“正度”的值是非负数。同学甲认为：可用式子|a-b|来表示“正度”，|a-b|的值越小，表示等腰三角形越接近正三角形；同学乙认为；可用式子|α-β|来表示“正度”，|α-β|的值越小，表示等腰三角形越接近正三角形。探究：(1)他们的方案哪个较为合理，为什么？(2)对你认为不够合理的方案，请加以改进(给出式子即可)(3)请再给出一种衡量“正度”的表达式

19、(黑龙江省　 2003年)如图1-15，已知：如图(1)，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD、AG⊥CE，垂足分别为F、G，连接FG，延长AF、AG，与直线BC相交，易证FG=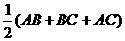。若(1)BD、CE分别是△ABC的内角平分线(图(2))；(2)BD为△ABC的内角平分线，CE为△ABC的外角平分线(图(3))，则在图(2)、图(3)两种情况下，线段FG与△ABC三边又有怎样的数量关系》请写出你的猜想，并对其中一种情况给予证明。

18、(江西省　 2003年)如图1-14，已知：A、D两点分别是正三角形DEF、正三角形ABC的中心，连接GH、AD，延长AD交BC于M，延长DA交EF于N，G是FD与AB的交点，H是ED与AC的交点。

(1)　　　 请写出三个不同类型、必须经过至少两步推理才能得到的正确结论(不要求写出证明过程)

(2)　　　 问FE、GH、BC有何位置关系？试证明你的结论。