1. (2006临安)抛物线y=3(x-1)+1的顶点坐标是(　　 )

A．(1，1)　　　　 B．(-1，1)　　　　 C．(-1，-1)　　　　 D．(1，-1)

6．二次函数与一元二次方程的关系：

　 (1)一元二次方程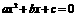就是二次函数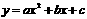当函数y的值为0时的情况．

　 (2)二次函数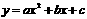的图象与x轴的交点有三种情况：有两个交点、有一个交点、没有交点；当二次函数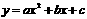的图象与x轴有交点时，交点的横坐标就是当y=0时自变量x的值，即一元二次方程ax²+bx+c=0的根．

　 (3)当二次函数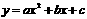的图象与 x轴有两个交点时，则一元二次方程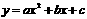有两个不相等的实数根；当二次函数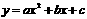的图象与x轴有一个交点时，则一元二次方程ax²+bx+c＝0有两个相等的实数根；当二次函数y＝ax²+ bx+c的图象与 x轴没有交点时，则一元二次方程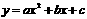没有实数根．　　　　　　　　　　　　　　　　　

典例精析

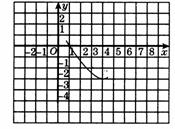
[例1](1) 已知抛物线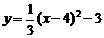 的部分图象如图，则

再次与x轴相交时的坐标是( 　　) 　

A．(5，0) B。(6，0)　

C．(7，0) D。(8，0)

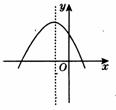
(2)已知二次函数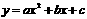的图象如图所示，则a、b、c满足(　 　)

　 A．a＜0，b＜0，c＞0　 B．a＜0，b＜0，c＜0

C．a＜0，b＞0，c＞0　 D．a＞0，b＜0，c＞0

[分析](1)由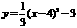，可知其对称轴为x=4,而图象与x轴已交于(1，0)，则与x轴的另一交点为(7，0)。

(2)由抛物线开口向下可知a＜0；与y轴交于正半轴可知c＞0；抛物线的对称轴在y轴左侧，可知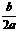－ ＜0．则b＜0．故选A．

[解答](1)C　 (2)A

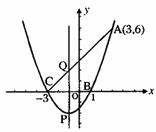[例2](2006宁波)如图，抛物线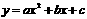与x轴相交于B(1，0)、C(-3，0)，且过点A(3，6)。

(1)　　　 求a，b，c的值。

(2)　　　 设抛物线的顶点为P，对称轴与线段AC相交于点Q，连结CP、PB、BQ。试求四边形PBQC的面积。

[分析]本题第(1)小题考察用待定系数法求抛物线的解析式，结合条件可以考虑用交点式。第(2)小题关键是求出Q点的坐标，因为它是对称轴与线段AC的交点，所以要先求出直线AC的解析式。

[解答](1)由题意可设：，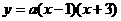

把点A(3，6)坐标代入可得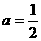　

所以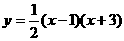，　 即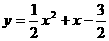

所以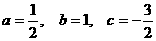

(2)　　　 顶点P的坐标为(-1，-2)，对称轴是直线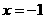

而直线AC的解析式为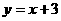

　 所以对称轴与线段AC的交点Q的坐标为(-1，2)

设对称轴与x轴相交于点D，则可得：DP=DB=DQ=DC=2

所以四边形PBQC的面积为8。

[例3]已知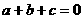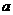，≠0，把抛物线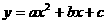向下平移1个单位，再向左平移5个单位所得到的新抛物线的顶点是(－2，0)，求原抛物线的解析式。

[分析]①由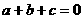可知：原抛物线的图像经过点(1，0)；②新抛物线向右平移5个单位，再向上平移1个单位即得原抛物线。

[解答]可设新抛物线的解析式为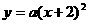，则原抛物线的解析式为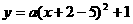，又易知原抛物线过点(1，0)

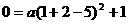∴，解得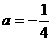

∴原抛物线的解析式为：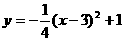

[例4]如图是抛物线型的拱桥，已知水位在AB位置时，水面宽米，水位上升3米就达到警戒水位线CD，这时水面宽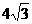米，若洪水到来时，水位以每小时0.25米的速度上升，求水过警戒线后几小时淹到拱桥顶？

[分析]本题关键是建立合适的直角坐标系。

[解答]以AB所在直线为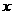轴，AB的中点为原点，建立直角坐标系，则抛物线的顶点M在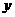轴上，且A(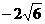，0)，B(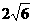，0)，C(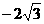，3)，D(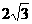，3)，设抛物线的解析式为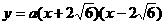，代入D点得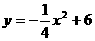，顶点M(0，6)，所以(小时)

[例5]已抛物线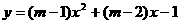(为实数)。

(1)为何值时，抛物线与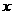轴有两个交点？

(2)如果抛物线与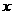轴相交于A、B两点，与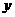轴交于点C，且△ABC的面积为2，求该抛物线的解析式。

[分析]抛物线与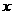轴有两个交点，则对应的一元二次方程有两个不相等的实数根，将问题转化为求一元二次方程有两个不相等的实数根应满足的条件。

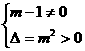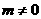[解答](1)由已知有，解得且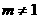

　　 (2)由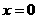得C(0，－1)

又∵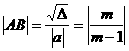

∴

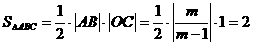
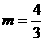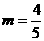
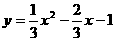∴或

∴或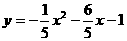

课内巩固

5．二次函数表达式的求法：

　 ⑴若已知抛物线上三点坐标，可利用待定系数法求得；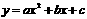

　 ⑵若已知抛物线的顶点坐标或对称轴方程，则可采用顶点式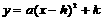：其中顶点为(h，k)对称轴为直线x=h；

　 ⑶若已知抛物线与x轴的交点坐标，则可采用交点式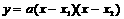：,其中与x轴的交点坐标为(x₁，0)，(x₂，0)

4. 二次函数的图象与系数的关系：

(1) a的符号：a的符号由抛物线的开口方向决定．抛物线开口向上，则a＞0；物线开口向下，则a＜0．

(2)b的符号出的符号由对称轴决定，若对称轴是y轴，则b=0；若对称轴在y轴左侧，则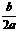－＜0即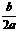＞0，则a、b为同号；若对称轴在y轴右侧，则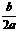－＞0，即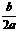＜0．则a、b异号．即“左同右异”．

(3)c的符号：c的符号由抛物线与y轴的交点位置确定．若抛物线交y轴于正半轴，则

c＞0，抛物线交y轴于负半轴．则c＜0；若抛物线过原点，则c=0．

(4)△的符号：△的符号由抛物线与x轴的交点个数决定．若抛物线与x轴只有一个交点，则△=0；有两个交点，则△＞0；没有交点，则△＜0 ．

3．图象的平移：将二次函数y=ax² (a≠0)的图象进行平移，可得到y=a(x－h)²+k的图象．

将y=ax²的图象向左(h<0)或向右(h＞0)平移|h|个单位，再向上(k>0)或向下(k<0)平移|k|个单位，即可得到y=a(x－h)² +k的图象，其顶点是(h，k)，对称轴是直线x=h，形状、开口方向与抛物线y=ax²相同．

2．二次函数的图象及性质：

　 (1)二次函数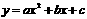的图象是一条抛物线．顶点为(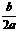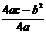－，)，对称轴x=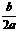－；当a＞0时，抛物线开口向上，图象有最低点，且x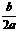＞－，y随x的增大而增大，x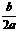＜－，y随x的增大而减小；当a＜0时，抛物线开口向下，图象有最高点，且x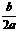＞－，y随x的增大而减小，x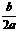＜－，y随x的增大而增大．

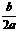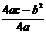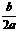　(2)当a＞0时，当x=－时，函数有最小值；当a＜0时，当x =－时，函数有最大值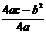

1．二次函数的定义：形如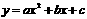(a≠0，a，b，c为常数)的函数为二次函数．

4、　 如图，四边形ABCD中，DE⊥AB，DF⊥BC，垂足分别为E、F，∠EDF=60°，CF=4cm，AE=2cm，求∠A，AB，AD。(8分)

3、　 已知：平行四边形ABCD 中，AB+BC=11cm，∠B=30°，平行四边形ABCD的面积是15cm²，求AB，BC。(8分)

2、　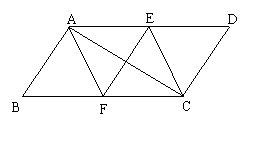 已知：如图平行四边形ABCD的对角线AC的垂直平分线交AD于E，交BC于F ，求证：四边形AFCE是菱形。(8分)