
题目列表(包括答案和解析)
5.一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图像可能是 ( )
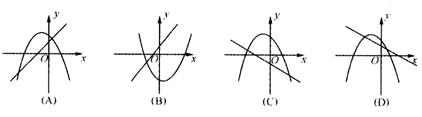
4.若直线y=ax+b (a≠0)在第二、四象限都无图像,则抛物线y=ax2+bx+c ( )
A.开口向上,对称轴是y轴 B.开口向下,对称轴平行于y轴
C.开口向上,对称轴平行于y轴 D.开口向下,对称轴是y轴
3.抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
A.-16 B.-4 C.8 D.16
2.设等边三角形的边长为x(x>0),面积为y,则y与x的函数关系式是( )
A.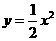 B.
B.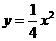 C.
C.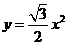 D.
D.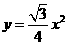
1.在下列关系式中,y是x的二次函数的关系式是 ( )
A.2xy+x2=1 B.y2-ax+2=0 C.y+x2-2=0 D.x2-y2+4=0
1. 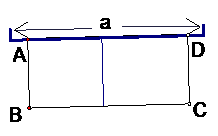 如图,有长为24米的篱笆,一面利用墙(墙的最大可利用长度a为10米)围成中间隔一道篱笆的长方形花圃。设花圃的宽AB为
如图,有长为24米的篱笆,一面利用墙(墙的最大可利用长度a为10米)围成中间隔一道篱笆的长方形花圃。设花圃的宽AB为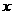 米,面积为
米,面积为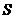 平方米。
平方米。
(1) 求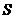 与
与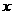 的函数关系式;
的函数关系式;
(2) 如果要围成面积为45平方米的花圃,AB的长是多少米?
(3) 能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由。
解:(1)花圃宽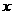 米,长为
米,长为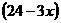 米,则它的面积
米,则它的面积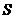 与
与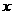 的函数关系式为
的函数关系式为
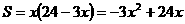 。
。
(2) 当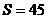 时,
时,
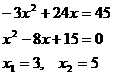
所以 , 当AB长为3米或5米时花圃的面积为45平方米。
(3)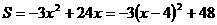
所以,能围成面积比45平方米更大的花圃,它的最大面积为48平方米。
上述解法正确吗?为什么?
16.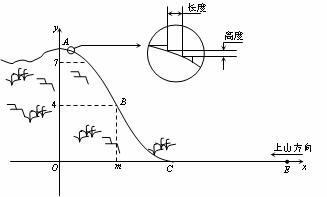 (2006嘉兴)某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为y=-
(2006嘉兴)某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为y=-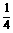 x2+8,BC所在抛物线的解析式为y=
x2+8,BC所在抛物线的解析式为y=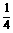 (x-8)2,且已知B(m,4).
(x-8)2,且已知B(m,4).
(1)设P(x,y)是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一起铺到山脚,为什么?
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道站的起点选择在山脚水平线上的点E处,OE=1600(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为y=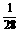 (x-16)2.试求索道的最大悬空高度.
(x-16)2.试求索道的最大悬空高度.
反思纠错
15.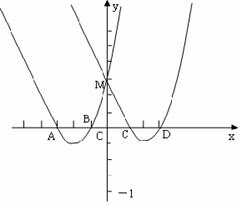 (2006大连)如图,抛物线E:y=x2+4x+3交x轴于A、B两点,交y轴于M点,抛物线E关于y轴对称的抛物线F交x轴于C、D两点。
(2006大连)如图,抛物线E:y=x2+4x+3交x轴于A、B两点,交y轴于M点,抛物线E关于y轴对称的抛物线F交x轴于C、D两点。
(1)求F的解析式;
(2)在x轴上方的抛物线F或E上是否存在一点N,使以A、C、N、M为顶点的四边形是平行四边形。若存在,求点N的坐标;若不存在,请说明理由;
(3)若将抛物线E的解析式改为y=ax2+bx+c ,试探索问题(2)。
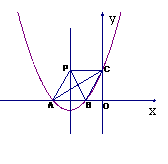
14.(2006台州)如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
(1)求此抛物线的对称轴及点A的坐标;
(2)过点C作x轴的平行线交抛物线的对称轴于点P,你能判断四边形ABCP是什么四边形吗?请证明你的结论;
 (3)连结AC,BP,若AC⊥BP,试求此抛物线的解析式.
(3)连结AC,BP,若AC⊥BP,试求此抛物线的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com