
题目列表(包括答案和解析)
3.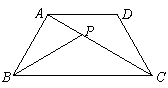 在等腰梯形ABCD中,AD∥BC,AD<BC,P是对角线AC
在等腰梯形ABCD中,AD∥BC,AD<BC,P是对角线AC
上的一点,且∠ABP=∠CAD,AB=4,BC=6.
(1)试找出所有相似的三角形,并分别予以证明;
(2)假设AD=x,BP=y,试求y与x的函数解析式,并写出它
的定义域;
(3)试探索:△ABP是否可能成为等腰三角形?如果可能,请求出此时x的值;如果不可能,请说明理由.
2.Rt△ABC(∠A=90°)在直角坐标系中的位置如图所示,
已知点C(1,4),tg∠CBA=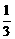 ,tg∠CBO=2.
,tg∠CBO=2.
(1)求点A的坐标及图象过点A、B、C的二次函数解析式.
(2)若(1)中的函数图象与x轴的负半轴交于点P,试判断
△AOP与△ABC是否相似?若相似,请证明;若不相似,请
说明理由.
1.已知二次函数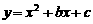 的顶点M在直线y=-4x上,并且图象经过点A(-1,0).
的顶点M在直线y=-4x上,并且图象经过点A(-1,0).
(1)求这个二次函数的解析式;
(2)设此二次函数与x轴的另一个交点为B,与y轴的交点为C,求经过M、B、C三点的圆O′的直径长;
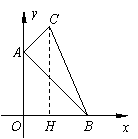 (3)设圆O′与y轴的另一个交点为N,经过P(-2,0)、N两点的直线为l,则圆心O′是否在直线l上?请说明理由.
(3)设圆O′与y轴的另一个交点为N,经过P(-2,0)、N两点的直线为l,则圆心O′是否在直线l上?请说明理由.
2. 左图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象(分别为正比例函数和一次函数).两地间的距离是80千米.请你根据图象回答或解决下面的问题:
左图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象(分别为正比例函数和一次函数).两地间的距离是80千米.请你根据图象回答或解决下面的问题:
(1)谁出发的较早?早多长时间?谁到达乙地较早?
早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)请你分别求出表示自行车和摩托车行驶过程的
函数解析式(不要求写出自变量的取值范围);
(4)指出在什么时间段内两车均行驶在途中(不包
括端点);在这一时间段内,请你分别按下列条件列
出关于时间x的方程或不等式(不要化简,也不要求
解):①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面.
1.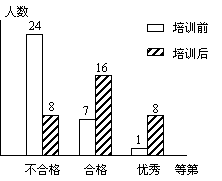 某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:
某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:
(1)这32名学生培训前考分的中位数所在的等级
是 ,培训后考分的中位数所在的等级
是 .
(2)这32名学生经过培训,考分等级“不合格”
的百分比由 下降到 .
(3)估计该校整个初二年级中,培训后考分等级为
“合格”与“优秀”的学生共有 名.
(4)你认为上述估计合理吗:理由是什么?
答: ,理由: .
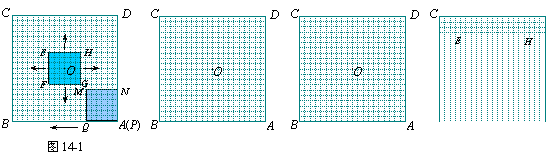
9、图14-1至图14-7的正方形霓虹灯广告牌ABCD都是20×20的等距网格(每个小方格的边长均为1个单位长),其对称中心为点O.
如图14-1,有一个边长为6个单位长的正方形EFGH的对称中心也是点O,它以每秒1个单位长的速度由起始位置向外扩大(即点O不动,正方形EFGH经过一秒由6×6扩大为8×8;再经过一秒,由8×8扩大为10×10;……),直到充满正方形ABCD,再以同样的速度逐步缩小到起始时的大小,然后一直不断地以同样速度再扩大、再缩小.
另有一个边长为6个单位长的正方形MNPQ从如图14-1所示的位置开始,以每秒1个单位长的速度,沿正方形ABCD的内侧边缘按A→B→C→D→A移动(即正方形MNPQ从点P与点A重合位置开始,先向左平移,当点Q与点B重合时,再向上平移,当点M与点C重合时,再向右平移,当点N与点D重合时,再向下平移,到达起始位置后仍继续按上述方式移动).
正方形EFGH和正方形MNPQ从如图14-1的位置同时开始运动,设运动时间为x秒,它们的重叠部分面积为y个平方单位.
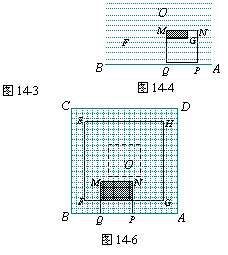
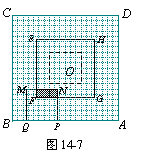
(1)请你在图14-2和图14-3中分别画出x为2秒、18秒时,正方形EFGH和正方形MNPQ的位置及重叠部分(重叠部分用阴影表示),并分别写出重叠部分的面积;
(2)①如图14-4,当1≤x≤3.5时,求y与x的函数关系式;
②如图14-5,当3.5≤x≤7时,求y与x的函数关系式;
③如图14-6,当7≤x≤10.5时,求y与x的函数关系式;
④如图14-7,当10.5≤x≤13时,求y与x的函数关系式.
(3)对于正方形MNPQ在正方形ABCD各边上移动一周的过程,请你根据重叠部分面积y的变化情况,指出y取得最大值和最小值时,相对应的x的取值情况,并指出最大值和最小值分别是多少.(说明:问题(3)是额外加分题,加分幅度为1-4分)
 |
|||
|
|||








 |
|||||||
 |
|||||||
|
|||||||
 |
|||||||
[解析]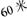
(1)相应的图形如图2-1,2-2.
当x=2时,y=3;
 当x=18时,y=18.
当x=18时,y=18.
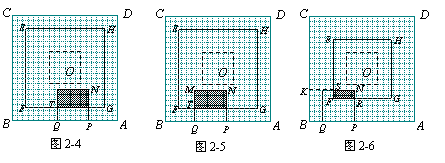
(2)①当1≤x≤3.5时,如图2-3,
延长MN交AD于K,设MN与HG交于S,MQ与FG交于T,则MK=6+x,SK=TQ=7-x,从而MS=MK-SK=2x-1,MT=MQ-TQ=6-(7-x)= x-1.
∴y=MT·MS=(x-1)(2x-1)=2x2-3x+1.
②当3.5≤x≤7时,如图2-4,设FG与MQ交于T,则
TQ=7-x,∴MT=MQ-TQ=6-(7-x)=x-1.
∴y=MN·MT=6(x-1)=6x-6.
③当7≤x≤10.5时,如图2-5,设FG与MQ交于T,则
TQ=x-7,∴MT=MQ-TQ=6-(x-7)=13-x.
∴y= MN·MT =6(13-x)=78-6x.
④当10.5≤x≤13时,如图2-6,设MN与EF交于S,NP交FG于R,延长NM交BC于K,则MK=14-x,SK=RP=x-7,
∴SM=SK-MK=2x-21,从而SN=MN-SM=27-2x,NR=NP-RP=13-x.
∴y=NR·SN=(13-x)(27-2x)=2x2-53x+351.
(说明:以上四种情形,所求得的y与x的函数关系式正确的,若不化简不扣分)
(3)对于正方形MNPQ,
 ①在AB边上移动时,当0≤x≤1及13≤x≤14时,y取得最小值0;
①在AB边上移动时,当0≤x≤1及13≤x≤14时,y取得最小值0;
当x=7时,y取得最大值36.
②在BC边上移动时,当14≤x≤15及27≤x≤28时,y取得最小值0;
当x=21时,y取得最大值36.
③在CD边上移动时,当28≤x≤29及41≤x≤42时,y取得最小值0;
当x=35时,y取得最大值36.
④在DA边上移动时,当42≤x≤43及55≤x≤56时,y取得最小值0;
当x=49时,y取得最大值36.
8、图10-1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图10-2是车棚顶部截面的示意图,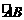 所在圆的圆心为O.
所在圆的圆心为O.
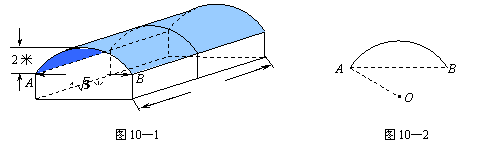 车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留
车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留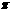 ).
).
[解析]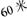
连结OB,过点O作OE⊥AB,垂足为E,交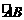 于F,如图1. …………(1分)
于F,如图1. …………(1分)
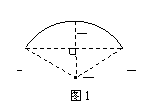 由垂径定理,可知: E是AB中点,F是
由垂径定理,可知: E是AB中点,F是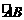 中点,
中点,
∴EF是弓形高 .
∴AE=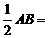 2
2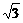 ,EF=2. …………(2分)
,EF=2. …………(2分)
设半径为R米,则OE=(R-2)米.
在Rt△AOE中,由勾股定理,得 R 2=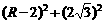 .
.
解得 R =4. ……………………………………………………………………(5分)
∵sin∠AOE=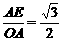 , ∴ ∠AOE=60°, ………………………………(6分)
, ∴ ∠AOE=60°, ………………………………(6分)
∴∠AOB=120°. ∴
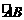 的长为
的长为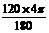 =
=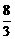
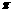 . ………………………(7分)
. ………………………(7分)
∴帆布的面积为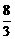
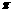 ×60=160
×60=160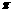 (平方米). …………………………………(8分)
(平方米). …………………………………(8分)
(说明:本题也可以由相交弦定理求圆的半径的长.对于此种解法,请参照此评分标准相应给分)
6、利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的二次函数关系式(不要求写出x的取值范围);
(3)请把(2)中的二次函数配方成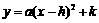 的形式,并据此说明,该经销店要
的形式,并据此说明,该经销店要
获得最大月利润,售价应定为每吨多少元;
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
[解析] (1)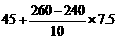 =60(吨).
=60(吨).
(2)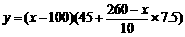 ,
,
化简得: 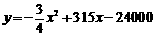 .
.
(3)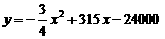
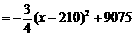 .
.
利达经销店要获得最大月利润,材料的售价应定为每吨210元.
(4)我认为,小静说的不对.
理由:方法一:当月利润最大时,x为210元,
而对于月销售额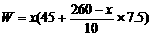
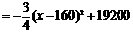 来说,
来说,
当x为160元时,月销售额W最大.
∴当x为210元时,月销售额W不是最大.
∴小静说的不对.
方法二:当月利润最大时,x为210元,此时,月销售额为17325元;
而当x为200元时,月销售额为18000元.∵17325<18000,
∴当月利润最大时,月销售额W不是最大.
∴小静说的不对.
(说明:如果举出其它反例,说理正确,也相应给分)
5、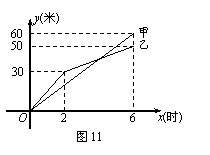 有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.图11是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.图11是反映所挖河渠长度y(米)与挖掘时间x(时)之间关系的部分图象.请解答下列问题:
(1)乙队开挖到30米时,用了_____小时.开挖6小时时,
甲队比乙队多挖了______米;
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数关系式;
②乙队在2≤x≤6的时段内,y与x之间的函数关系式;
③开挖几小时后,甲队所挖掘河渠的长度开始超过乙队?
(3)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.问甲队从开挖到完工所挖河渠的长度为多少米?
[解析] (1)2;10;
(2)①设甲队在0≤x≤6的时段内y与x之间的函数关系式为y=k1x,
由图可知,函数图象过点(6,60),
∴6 k1=60,解得k1=10,
∴y =10x.
②设乙队在2≤x≤6的时段内y与x之间的函数关系式为y =k2x+b,
由图可知,函数图象过点(2,30)、(6,50),
∴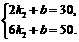 解得
解得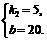
∴y =5x+20.
③由题意,得10x>5x+20,解得x>4.
所以,4小时后,甲队挖掘河渠的长度开始超过乙队.
(说明:通过观察图象并用方程来解决问题,正确的也给分)
(3)由图可知,甲队速度是:60÷6=10(米/时).
设甲队从开挖到完工所挖河渠的长度为z米,依题意,得
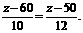
解得 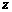 =110.
=110.
答:甲队从开挖到完工所挖河渠的长度为110米.
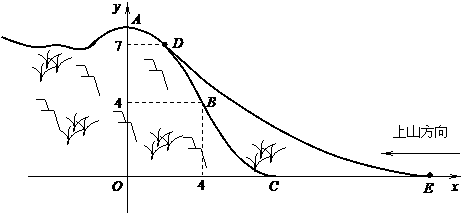
4、某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为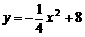 ,BC所在抛物线的解析式为
,BC所在抛物线的解析式为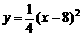 ,且已知
,且已知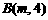 .
.
(1)设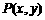 是山坡线AB上任意一点,用y表示x,并求点B的坐标;
是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一直铺到山脚,为什么?
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,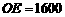 (米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为
(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为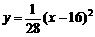 .试求索道的最大悬空高度.
.试求索道的最大悬空高度.

[解析] (1)∵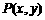 是山坡线AB上任意一点,
是山坡线AB上任意一点,
∴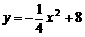 ,
,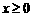 , (…2分)
, (…2分)
∴ ,
,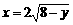 (…3分)
(…3分)
∵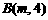 ,∴
,∴ =4,∴
=4,∴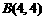 (…4分)
(…4分)
(2)在山坡线AB上,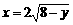 ,
,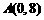
①令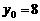 ,得
,得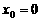 ;令
;令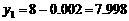 ,得
,得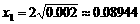
∴第一级台阶的长度为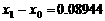 (百米)
(百米)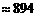 (厘米) (…6分)
(厘米) (…6分)
同理,令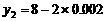 、
、 ,可得
,可得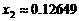 、
、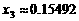
∴第二级台阶的长度为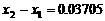 (百米)
(百米)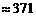 (厘米) (…7分)
(厘米) (…7分)
第三级台阶的长度为 (百米)
(百米)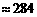 (厘米) (…8分)
(厘米) (…8分)
②取点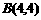 ,又取
,又取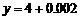 ,则
,则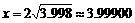
∵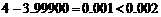
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚 (…10分)
(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性)
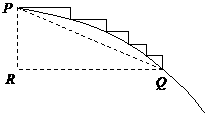 ②另解:连接任意一段台阶的两端点P、Q,如图
②另解:连接任意一段台阶的两端点P、Q,如图
∵这种台阶的长度不小于它的高度
∴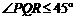
当其中有一级台阶的长大于它的高时,
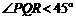 (…9分)
(…9分)
在题设图中,作 于H
于H
则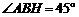 ,又第一级台阶的长大于它的高
,又第一级台阶的长大于它的高
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚 (…10分)
 (3)
(3)
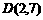 、
、 、
、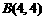 、
、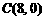
由图可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值(…11分)
索道在BC上方时,悬空高度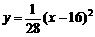
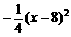
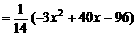
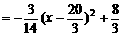 (…13分)
(…13分)
当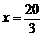 时,
时,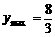
∴索道的最大悬空高度为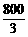 米.
米.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com