
题目列表(包括答案和解析)
2.反比例函数的图象及性质:
|
表达式 |
y=(k≠0) |
|
|
图 象 |
k>0 |
k<0 |
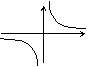 |
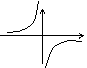 |
|
|
性 质 |
1.图象在第一、三象限; 2.每个象限内,函数y的值随x的增大而减小. |
1.图象在第二、四象限; 2.在每个象限内,函数y值随x的增大而增大. |
典例精析
[例1](2006黄冈)反比例函数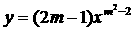 ,当x>0时,y随x的增大而增大,则m的值时( )
,当x>0时,y随x的增大而增大,则m的值时( )
A、±1 B、小于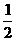 的实数 C、-1 D、1
的实数 C、-1 D、1
[分析]本题考察反比例函数的定义及有关性质。反比例函数不仅有形式: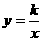 (k ≠0),也可以改写成:
(k ≠0),也可以改写成: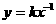 (k ≠0)。 又因为当x>0时,y随x的增大而增大,所以k<0。
(k ≠0)。 又因为当x>0时,y随x的增大而增大,所以k<0。
[解答]由题意可得: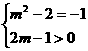 ,解得
,解得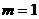 .因此选D。
.因此选D。
[例2](1)已知y与(2x+1)成反比例,且当x=1时,y=2,那么当x=0时,y=__________。
(2) 如果反比例函数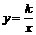 的图象经过点(―3,1),那么k=______。
的图象经过点(―3,1),那么k=______。
(3)若点(3,4)是反比例函数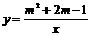 图象上一点,则此函数图象必经过点( )。
图象上一点,则此函数图象必经过点( )。
A.(2,6) B。(2,―6) C。(4,―3) D。(3,―4)
[分析]以上几题考查了反比例函数的定义和利用待定系数法求反比例函数的解析式。
[解答](1)依题意设y=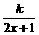 ,∴当x=1时,y=
,∴当x=1时,y=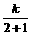 =2。
=2。
∴k=6, 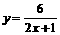 ,故当x=0时,
,故当x=0时,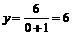 。
。
(2)依题意得:当x=―3时,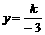 =1。 ∴k=―3。
=1。 ∴k=―3。
(3)由题意得:当x=3时,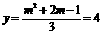 。
。
∴ ,y=
,y=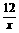 。 故选A。
。 故选A。
注意:第(3)题要注意把m2+2m―1看作一个整体,体现了整体代入的思想。
[例3](1)反比例函数y=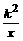 (k≠0)的图象的两个分支分别位于 ( )
(k≠0)的图象的两个分支分别位于 ( )
A:第一、二象限 B:第一、三象限 C:第二、四象限 D:第一、四象限
(2) 设有反比例函数y=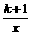 。 (x1,y1)、(x2,y2)为其图象上两点,当x1<0<x2时,有y1>y2 ,则k的取值范围是______。
。 (x1,y1)、(x2,y2)为其图象上两点,当x1<0<x2时,有y1>y2 ,则k的取值范围是______。
(3)当k<0时,反比例函数y=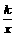 和一次函数y=kx+2的图象在致是图中的( )。
和一次函数y=kx+2的图象在致是图中的( )。

[分析]以上几题考查了反比例函数的图象及其性质。
[解答](1)∵k≠0, ∴k2>0,双曲线分布在一、三象限。选B。
(2)∵x1<0<x2时,有y1>y2∴画草图可知双曲线的图象分布在二、四象限,k+1<0。故填k<―1。
 (3)∵k<0, ∴反比例函数的图象落在二、四象限,一次函数 y随x的增大而减少。又y=kx+2的图象经过点(0,2),故选B。
(3)∵k<0, ∴反比例函数的图象落在二、四象限,一次函数 y随x的增大而减少。又y=kx+2的图象经过点(0,2),故选B。
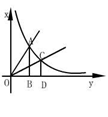
[例4]如图,正比例函数y=x及y=mx的图象与反 比例函数y= 的图象分别交于第一象限内的A、C两点,过A、C分别向x轴作垂线,垂足分别为B、D。若直角三角形AOB与直角三角形COD的面积分别为S1、S2,则S1与S2的关系为( )。
的图象分别交于第一象限内的A、C两点,过A、C分别向x轴作垂线,垂足分别为B、D。若直角三角形AOB与直角三角形COD的面积分别为S1、S2,则S1与S2的关系为( )。
A.S1>S2 B。S1=S2 C。S1<S2 D。与m、k的值有关
[分析]此题考查了反比例函数同一次函数、几何中的面积等知识相结合的综合问题。
[解答]设A、B的坐标为A(x1,y1)、B(x2,y2)。
则y1=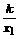 ,y2=
,y2= 。即x1·y1 =k,x2·y2=k
。即x1·y1 =k,x2·y2=k
∵OB=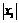 ,AB=
,AB=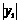 ,OD=
,OD=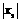 ,CD=
,CD=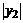 。
。
∴S1=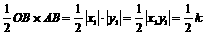 , S2=
, S2=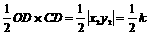 。故选B。
。故选B。
由此我们可以得出:过反比例函数y= 的图象图象上任一点,向x轴作垂线,这一点与垂足、原点所得到的直角三角形,其面积为
的图象图象上任一点,向x轴作垂线,这一点与垂足、原点所得到的直角三角形,其面积为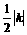 ;若再向y轴作垂线,此时围成的矩形面积为
;若再向y轴作垂线,此时围成的矩形面积为 。
。
[例5](2005江苏南京)一定质量的氧气,它的密度ρ(千克/米3)是它的体积V(立方米)的反比例函数,当V=10立方米时,ρ=1.43千克/米3
(1)求ρ与V的函数关系式。
(2)求当V=2立方米时氧气的密度ρ。
[分析]本题与自然科学的相关知识联系在一起,属于一道学科综合题。题目本身其实比较简单,还是用待定系数法求反比例函数的解析式。
[解答]解:(1)设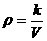 ,由题意可得:
,由题意可得: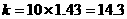
所以
(2)当V=2立方米时氧气的密度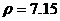 千克/米3
千克/米3
课内巩固
1. 反比例函数:若两个变量x、y间的关系式可以表示成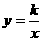 (k ≠0)的形式,则称y是x的反比例函数。
(k ≠0)的形式,则称y是x的反比例函数。
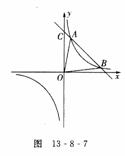
4.如图13-8-7已知一次函数 和反比例函数
和反比例函数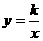 图象在第一象限内有两个不同的公共点A、B.
图象在第一象限内有两个不同的公共点A、B.
(1)求实数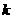 的取值范围;(2)若ΔAOB的面积S=24,求
的取值范围;(2)若ΔAOB的面积S=24,求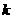 的值.
的值.
3、已知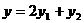 ,
,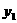 与
与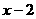 成正比例,
成正比例,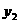 与
与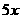 成反比例,且当
成反比例,且当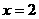 时,
时,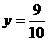 ;当
;当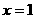 时,
时, ;求
;求 与
与 之间的函数解析式。
之间的函数解析式。
2、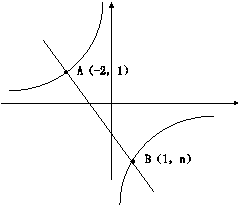 如图,一次函数
如图,一次函数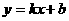 的图像与反比例函数
的图像与反比例函数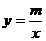 的图像相交于A、B两点,
的图像相交于A、B两点,
(1)利用图中条件,求反比例函数和一次函数的解析式
(2)根据图像写出使一次函数的值大于反比例函数的值的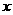 的取值范围。
的取值范围。
1、在某一电路中,保持电压U不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流I=2安培。
(1)求I与R之间的函数关系式
(2)当电流I=0.5安培时,求电阻R的值;
10、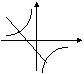
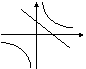
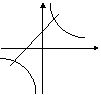
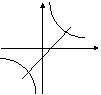 在同一坐标系中,函数
在同一坐标系中,函数 和
和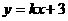 的图像大致是 ( )
的图像大致是 ( )
A B C D
9、已知反比例函数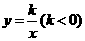 的图像上有两点A(
的图像上有两点A(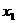 ,
,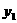 ),B(
),B(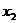 ,
,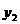 ),且
),且 ,则
,则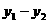 的值是( )
的值是( )
A、正数 B、负数 C、非正数 D、不能确定
8、 如图 ,A、C是函数
如图 ,A、C是函数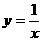 的图象上的任意两点,过A作
的图象上的任意两点,过A作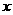 轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,RtΔCOD的面积为S2则 ( )
轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,RtΔCOD的面积为S2则 ( )
A. S1 >S2 B. S1 <S2
C. S1=S2 D. S1与S2的大小关系不能确定
7、在同一直角坐标平面内,如果直线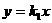 与双曲线
与双曲线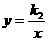 没有交点,那么
没有交点,那么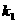 和
和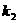 的关系一定是( )
的关系一定是( )
A. 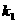 +
+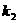 =0 B.
=0 B.
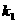

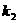 <0 C.
<0 C.
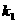

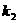 >0 D.
>0 D.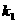 =
=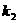
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com