
题目列表(包括答案和解析)
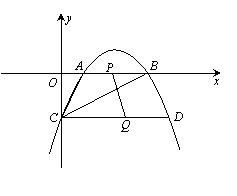
14.如图,抛物线y=-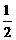 x2+
x2+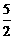 x-2与x轴相交于点A、B,与y轴相交于点C.
x-2与x轴相交于点A、B,与y轴相交于点C.
(1)求证:△AOC∽△COB;
(2)过点C作CD∥x轴交抛物线于点D.若点P在线段AB上以每秒1个单位的速度由A向B运动,同时点Q在线段CD上也以每秒1个单位的速度由D向C运动,则经过几秒后,PQ=AC.
13、在平面直角坐标系xoy中,抛物线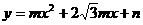 经过P(
经过P(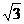 ,5),A(0,2)两点。(1)求次抛物线解析式;(2)设抛物线顶点为B,将直线AB沿y轴向下平移两个单位的直线L,直线L与抛物线的对称轴交于C点,求直线的解析式;(3)在(2)的条件下,求到直线OB,OC,BC距离相等的点的坐标。
,5),A(0,2)两点。(1)求次抛物线解析式;(2)设抛物线顶点为B,将直线AB沿y轴向下平移两个单位的直线L,直线L与抛物线的对称轴交于C点,求直线的解析式;(3)在(2)的条件下,求到直线OB,OC,BC距离相等的点的坐标。

12、已知:抛物线 顶点在直线
顶点在直线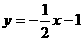 上,且仅当0﹤x﹤4时,y﹤0,设点A是抛物线与x轴的一个交点,点A在y轴的右侧,P为抛物线上的一个动点,
上,且仅当0﹤x﹤4时,y﹤0,设点A是抛物线与x轴的一个交点,点A在y轴的右侧,P为抛物线上的一个动点,
(1)求这个抛物线的解析式;(2)当△POA面积为5时,求点P坐标。(3)当cos∠OPA=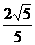 时,⊙M经过点O,A,P,求过A点且与⊙M相切的直线解析式
时,⊙M经过点O,A,P,求过A点且与⊙M相切的直线解析式

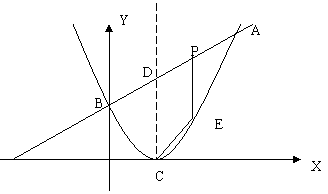
11、如图,已知二次函数图象顶点为C(1,0),直线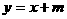 与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上,(1)求m值及这个二次函数关系式;(2)P为线段AB上一动点(P不与A,B重合),过P做x轴垂线与二次函数交于点E,设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式,并写出自变量x取值范围;(3)D为AB线段与二次函数对称轴的的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形?若存在,请求出P点坐标;若不存在,请说明理由。
与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上,(1)求m值及这个二次函数关系式;(2)P为线段AB上一动点(P不与A,B重合),过P做x轴垂线与二次函数交于点E,设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式,并写出自变量x取值范围;(3)D为AB线段与二次函数对称轴的的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形?若存在,请求出P点坐标;若不存在,请说明理由。
10、(2007四川成都)在平面直角坐标系 中,已知二次函数
中,已知二次函数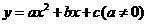 的图象与
的图象与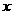 轴交于
轴交于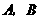 两点(点
两点(点 在点
在点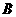 的左边),与
的左边),与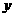 轴交于点
轴交于点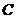 ,其顶点的横坐标为1,且过点
,其顶点的横坐标为1,且过点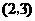 和
和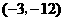 .
.
(1)求此二次函数的表达式;
(2)若直线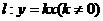 与线段
与线段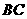 交于点
交于点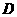 (不与点
(不与点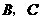 重合),则是否存在这样的直线
重合),则是否存在这样的直线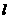 ,使得以
,使得以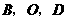 为顶点的三角形与
为顶点的三角形与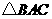 相似?若存在,求出该直线的函数表达式及点
相似?若存在,求出该直线的函数表达式及点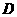 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
 (3)若点
(3)若点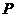 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角
是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角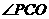 与
与 的大小(不必证明),并写出此时点
的大小(不必证明),并写出此时点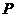 的横坐标
的横坐标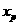 的取值范围.
的取值范围.
.
9、已知:以直线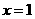 为对称轴的抛物线与
为对称轴的抛物线与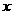 轴交于
轴交于 、
、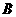 两点(点
两点(点 在点
在点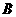 的左边),且经过点
的左边),且经过点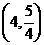 和
和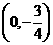 . 点
. 点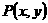 在抛物线的顶点
在抛物线的顶点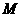 的右侧的半支上(包括顶点
的右侧的半支上(包括顶点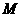 ),在
),在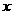 轴上有一点
轴上有一点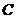 使
使 是等腰三角形,
是等腰三角形, .
.
(1)若 是直角,求点
是直角,求点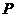 的坐标;
的坐标;
(2)当点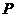 移动时,过点
移动时,过点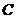 作
作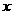 轴的垂线,交直线
轴的垂线,交直线 于点
于点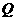 ,设
,设 的面积为
的面积为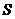 ,求
,求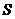 关于
关于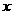 的函数解析式和自变量
的函数解析式和自变量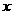 的取值范围,并画出它的图象.
的取值范围,并画出它的图象.
8、已知二次函数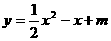 的图象经过点A(-3,6),并与
的图象经过点A(-3,6),并与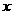 轴交于B、C两点(点B在C的左边),P为它的顶点.
轴交于B、C两点(点B在C的左边),P为它的顶点.
(1)试确定 的值;
的值;
(2)设点D为线段OC上的一点,且满足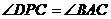 ,求直线AD的解析式;
,求直线AD的解析式;
(3)在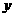 轴的正半轴上是否存在点M,使
轴的正半轴上是否存在点M,使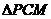 为等腰三角形,若存在,求出所有满足条件的点M的坐标,若不存在,请说明理由.
为等腰三角形,若存在,求出所有满足条件的点M的坐标,若不存在,请说明理由.
7、数学活动小组接受学校的一项任务:在紧靠围墙的空地上,利用围墙及一段长为60米的木栅栏围成一块生物园地,请设计一个方案使生物园的面积可能大。
(1)活动小组提交如图的方案。设靠墙的一边长为 x 米,则不靠墙的一边长为(60-2x)米,面积y= (60-2x) x米2.当x=15时,y最大值 =450米2。
(2)机灵的小明想:如果改变生物园的形状,围成的面积会更大吗?请你帮小明设计两个方案,要求画出图形,算出面积大小;并找出面积最大的方案.

6、如图,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0,6 ),D ( 4,6),且AB=2
(1)求点B的坐标;(2)求经过A、B、D三点的抛物线的解析式;
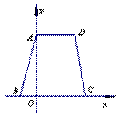 (3)在(2)中所求的抛物线上是否存在一点P,使得S△PBD=S梯形ABCD。若存在,请求出该点坐标,若不存在,请说明理由.
(3)在(2)中所求的抛物线上是否存在一点P,使得S△PBD=S梯形ABCD。若存在,请求出该点坐标,若不存在,请说明理由.
5、已知抛物线y=(1-m)x2+4x-3开口向下,与x轴交于A(x1,0)和B(x2,0)两点,其中xl<x2.
(1)求m的取值范围;
(2)若x12+ x22=10,求抛物线的解析式,并在给出的直角坐标系中画出这条抛物线;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com