
题目列表(包括答案和解析)
7、下列四个函数中,y随x增大而减小的是( )
A、y=2x B、y=-2x C、y=x2 D、 y=-x2
6、把函数y=-2x2的图象沿x轴对折,得到的图象的解析式为( )。
A、y=-2x2 B、y=2x2 C、y=-2(x+1)2 D、y=-2(x-1)2
5、下列函数中,是二次函数的是( )
A.y=8x2+1 B.y=8x+1;
C.y=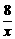 D.y=
D.y=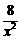
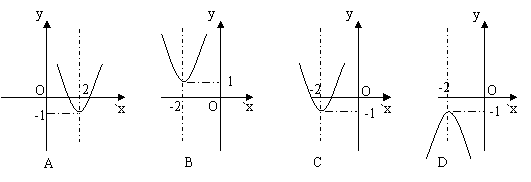
4、二次函数y=2(x+2)2-1的图象是( )。
3、把函数y=-3x2的图象沿x轴向右平移5个单位,得到的图象的解析式为( )。
A、y=-3x2+5 B、y=-3x2-5 C、y=-3(x+5)2 D、y=-3(x-5)2
2、开口向上,顶点坐标为(-9,3)的抛物线为( )。
A、y=2(x-9)2-3 B、y=2(x+9)2+3
C、y=-2(x-9)2-3 D、y=-2(x+9)2+3
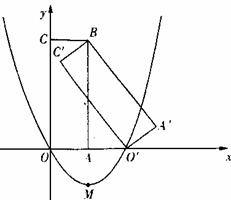
1、二次函数y=ax2+bx+c的图象如右图所示,根据图象可
得a、b、c与零的大小关系是( )
A、a>0,b<0,c>0 B、a>0,b>0,c>0
C、a<0,b<0,c<0 D、a<0,b>0,c<0
17、(2007山东威海)如图①,在平面直角坐标系中,点 的坐标为
的坐标为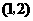 ,点
,点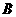 的坐标为
的坐标为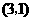 ,二次函数
,二次函数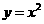 的图象记为抛物线
的图象记为抛物线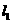 .
.
(1)平移抛物线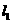 ,使平移后的抛物线过点
,使平移后的抛物线过点 ,但不过点
,但不过点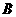 ,写出平移后的一个抛物线的函数表达式:
(任写一个即可).
,写出平移后的一个抛物线的函数表达式:
(任写一个即可).
(2)平移抛物线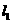 ,使平移后的抛物线过
,使平移后的抛物线过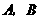 两点,记为抛物线
两点,记为抛物线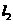 ,如图②,求抛物线
,如图②,求抛物线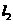 的函数表达式.
的函数表达式.
(3)设抛物线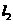 的顶点为
的顶点为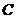 ,
, 为
为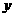 轴上一点.若
轴上一点.若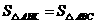 ,求点
,求点 的坐标.
的坐标.
(4)请在图③上用尺规作图的方式探究抛物线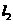 上是否存在点
上是否存在点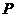 ,使
,使 为等腰三角形.若存在,请判断点
为等腰三角形.若存在,请判断点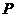 共有几个可能的位置(保留作图痕迹);若不存在,请说明师.
共有几个可能的位置(保留作图痕迹);若不存在,请说明师.
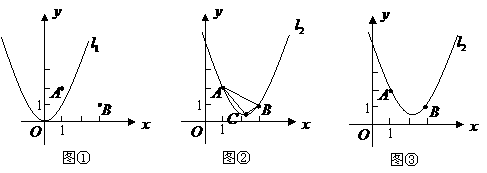
16、(2007四川眉山)如图,矩形A’BC’O’是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的.O’点在x轴的正半轴上,B点的坐标为(1,3).
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O、O’两点且图象顶点M的纵坐标为
-1.求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点P,使得ΔPOM为直角三角形?若存在,请求出P点的坐标和ΔPOM的面积;若不存在,请说明理由;
(3)求边C’O’所在直线的解析式.
15.将一矩形纸片OABC放在直角坐标系中,O为原点,C在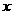 轴上,OA=6,OC=10.
轴上,OA=6,OC=10.
⑴如图⑴,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标;
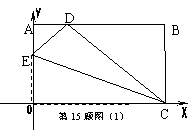
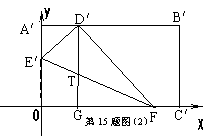
⑵如图⑵,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上的D′点,过D′作D′G∥A′O交E′F于T点,交OC′于G点,求证:TG=A′E′
⑶在⑵的条件下,设T(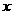 ,
,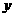 )①探求:
)①探求: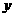 与
与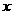 之间的函数关系式.②指出变量
之间的函数关系式.②指出变量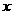 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com