4．已知正方形的面积为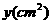，周长为x(cm)．

(1)请写出y与x的函数关系式；

(2)判断y是否为x的二次函数．

3．已知抛物线经过(2，0)、(3， 0)两，且经过(5，2)，求抛物线的解析式．

2．已知抛物线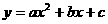的对称轴为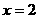，且经过点(1，4)和点(5，0)，则该抛物线的解析式为　　　　 　　　　　；

1.二次函数在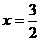时，有最小值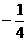，且函数的图象经过点(,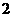)，则此函数的解析式为________________________.

3、二次函数的平移规律

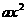
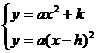
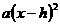y= y=+k

抛物线y=ax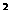+bx+c(a≠0)可由抛物线y=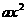平移得到，由于平移时，抛物线上所有点的移动规律都相同，所以只需研究其顶点的移动情况，因此有关抛物线的平移问题需要利用二次函数的顶点式:y=a(x-h)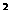+k(a≠0)来讨论，所以应先把二次函数化为顶点式然后再来平移；加减常数k(k＞0)，上下移动，即加上k则向上移动,减去k则向下移动；加减常数h(h＞0)，左右移动，即加上h则向左移动,减去h则向右移动；

2、二次函数的解析式求法：

用待定系数法可求出二次函数的解析式，确定二次函数的解析式一般需要三个独立的条件，根据不同的条件选用不同的设法：

(1)　 设一般式:y=ax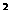+bx+c　(a≠0)

若已知条件是图象上一般的三个点，则设所求的二次函数为y=ax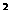+bx+c(a≠0)，将已知条件代入组成三元一次方程组，求出a、b、c的值．

(2)　 设顶点式:y=a(x-h)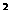+k(a≠0)

若已知二次函数的顶点坐标(h,k)，设所求二次函数为y=a(x+h)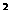+k(a≠0)，将第二个点的坐标代入，求出待定系数a，最后化为一般式．

(3)　 设交点式:y=a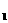(x-x)(x-x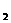)(a≠0)

已知二次函数的图象与X轴的两个交点的坐标为(x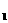,0),( x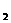,0)，设所求的二次函数为y=a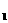(x-x)(x-x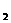)(a≠0)，将第三点坐标代入，求出待定系数a，最后化为一般式．

1、二次函数三种表达方式；

(1)　 一般式:y=ax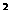+bx+c　(a≠0)

(2)　 顶点式:y=a(x-h)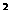+k(a≠0)

(3)　 交点式:y=a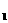(x-x)(x-x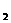)(a≠0)

求二次函数的解析式常常在解答题中出现，而平移常常在选择填空中出现．

(1)　 通过对实际问题情景的分析确定二次函数的表达式，并体会二次函数的意义。

(2)　 能够根据题目要求求出二次函数的解析式．

(3)　 能够根据题目要求确定平移后的解析式．

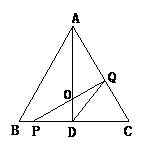
15、如图，在等边△ABC中，已知AB＝BC＝CA＝4cm，AD⊥BC于D，点P.Q分别从B.C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点P沿CA.AB向终点B运动，速度为2cm/s，设它们运动的时间为x(s)。

⑴ 求x为何值时，PQ⊥AC；

⑵ 设△PQD的面积为y(cm²)，当0＜x＜2时，求y与x的函数关系式；

⑶ 当0＜x＜2时，求证：AD平分△PQD的面积；

⑷ 探索以PQ为直径的圆与AC的位置关系。请写出相应位置关系的x的取值范围(不要求写出过程)

第　 20 课　 二次函数的解析式的求法和平移