
题目列表(包括答案和解析)
17、张老师骑摩托车的速度为45 km/h ,学生步行的速度是5km/h,学校与车站相距15km.如果2名学生要在55min从学校到车站,请张老师用摩托车送,但摩托车后座只能坐一人,学生不能架车,请你设计一个方案(学生只能步行或乘摩托车,上下摩托车的时间不计),使2名学生能在55分钟内全部到达车站,并用方程的有关知识说明理由.
你的方案是:
你的最佳方案是:
写出你认为是最佳方案的理由及解答.
16、某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将商品价格提高到原来的2.5倍,再作三次降价处理:第一次降价30%,标出 “亏本价” ;第二次降价30%,标出“破产价” ;第三次降价30%,标出“跳楼价”。三次降价处理销售结果如下表:

问:(1)“跳楼价”占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪一种方案更盈利?
15、某种化肥在县城里的甲、乙两个生产资料门市部均有销售,现了解到该种化肥在甲、乙两个门市部的标价均为600元/吨,但都有一定的优惠政策,甲门市部是第一吨按标价收费,超出部分每吨优惠25%;乙门市部每吨优惠20%出售
 .(1)写出甲门市部每次交易的销售额 (元)与销量x(吨)之间的函数关系式及乙门市部每次交易的销售额 (元)与销量x(吨)之间的函数关系式.
.(1)写出甲门市部每次交易的销售额 (元)与销量x(吨)之间的函数关系式及乙门市部每次交易的销售额 (元)与销量x(吨)之间的函数关系式.
(2)种粮大户张某想一次购买此种化肥4吨,李某想一次购买此种化肥8吨,他们到哪个门市部购买省钱,请给他们分别提出合理建议.
14、已知∆ABC(如下图),∠B=∠C=30°.请设计 三种不同的分法,将∆ABC分割成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形.请画出分割线段,标出能够说明分法的所得三角形的顶点和内角度数(或记号), 并在各种分法的空格线上填空.(画图工直不限,不要求证明,不要求写出画法)(注:不同分法是指只要有一条分割线段位置不同,就认为是不同的分法)




|
(1)求这块铁皮的面积(结果精确到1 )
(2)假如要制作的圆锥是一个无底面的模型,且使三角形
铁皮的利用率最高,请你画出裁剪方案的草图,并计算出
铁皮的利用率(精确到1%);
(3)假如要用这块铁皮裁一块完整的圆形和一块完整的扇
形,使之配套,恰好做成一个封闭圆锥模型,且使铁皮得
到充分利用,请你设计一种裁剪方案,画出草图,并计
算出铁皮的利用率(精确到1%)。
13、 某一广场进行装修,所用三种板材a=0.5
×0.5,b=0.5×0.2,c=0.2×0.2,规格如下图所示(单位:米)
某一广场进行装修,所用三种板材a=0.5
×0.5,b=0.5×0.2,c=0.2×0.2,规格如下图所示(单位:米)


(1)根据铺设部分面积的不同大小,设计下列有一定规律的图案(如图1、图2、图3),中间部分由a种板材镶边。

 ①请直接写出图2的面积 ;
①请直接写出图2的面积 ;
②若某一正方形图案的面积为11.56m²,求该图案每边有b种板材多少块?




26.(12分)已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
解:(1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
 ∴点B的坐标为(2,0),点C的坐标为(0,8)
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2
∴由抛物线的对称性可得点A的坐标为(-6,0)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上∴c=8,将A(-6,0)、B(2,0)代入表达式,得
解得
∴所求抛物线的表达式为y=-x2-x+8
(3)依题意,AE=m,则BE=8-m,
∵OA=6,OC=8,∴AC=10
∵EF∥AC ∴△BEF∽△BAC∴= 即=∴EF=
过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=
∴= ∴FG=·=8-m
∴S=S△BCE-S△BFE=(8-m)×8-(8-m)(8-m)
=(8-m)(8-8+m)=(8-m)m=-m2+4m
自变量m的取值范围是0<m<8
(4)存在.理由:∵S=-m2+4m=-(m-4)2+8 且-<0,
∴当m=4时,S有最大值,S最大值=8
∵m=4,∴点E的坐标为(-2,0)
∴△BCE为等腰三角形.
解:(1)令x=0,得y=-2 ∴C(0,一2).∵ACB=90°,CO⊥AB,.
∴ △AOC ∽△COB,.∴OA·OB=OC2;∴
OB= ∴m=4.
∴m=4.
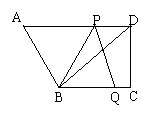
解(1)如图3,过点P作PM⊥BC,垂足为M,则四边形PDCM为矩形。∴PM=DC=12 ∵QB=16-t,∴S=
∵QB=16-t,∴S=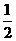 ×12×(16-t)=96-t
×12×(16-t)=96-t
(2)由图可知:CM=PD=2t,CQ=t。热以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ。在Rt△PMQ中,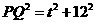 ,由PQ2=BQ2 得
,由PQ2=BQ2 得 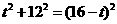 ,解得t=
,解得t=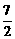 ;
;
|
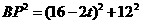 。由BP2=BQ2 得:
。由BP2=BQ2 得:
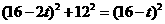 即
即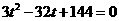 。
。
由于Δ=-704<0
∴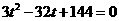 无解,∴PB≠BQ
无解,∴PB≠BQ
③若PB=PQ。由PB2=PQ2,得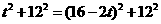
整理,得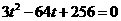 。解得
。解得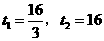 (不合题意,舍去)
(不合题意,舍去)
综合上面的讨论可知:当t=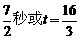 秒时,以B、P、Q三点为顶点的三角形是等腰三角形。
秒时,以B、P、Q三点为顶点的三角形是等腰三角形。
 (3)如图4,由△OAP∽△OBQ,得
(3)如图4,由△OAP∽△OBQ,得
∵AP=2t-21,BQ=16-t,∴2(2t-21)=16-t。
∴t=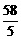 。
。
过点Q作QE⊥AD,垂足为E,
∵PD=2t,ED=QC=t,∴PE=t。
在RT△PEQ中,tan∠QPE=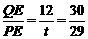
 (4)设存在时刻t,使得PQ⊥BD。如图5,过点Q作QE⊥ADS,垂足为E。由Rt△BDC∽Rt△QPE,得
(4)设存在时刻t,使得PQ⊥BD。如图5,过点Q作QE⊥ADS,垂足为E。由Rt△BDC∽Rt△QPE,得
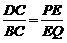 ,即
,即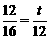 。解得t=9
。解得t=9
所以,当t=9秒时,PQ⊥BD。
25.(12分)如图 ,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒)。
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(3)当线段PQ与线段AB相交于点O,且2AO=OB时,求∠BQP的正切值;
 (4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由。
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由。
24. (10分)设抛物线
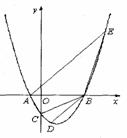
(10分)设抛物线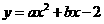 与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
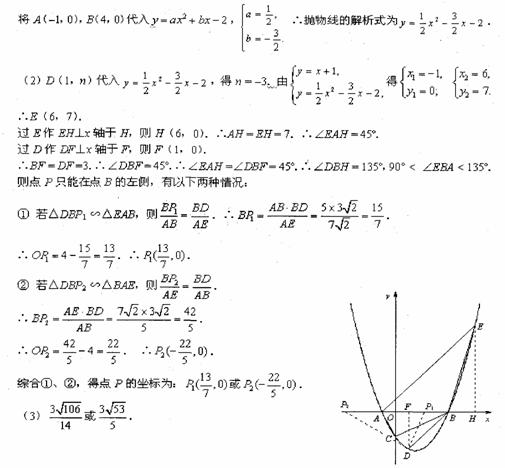
(2)已知点D(1,n )在抛物线上,过点A的直线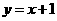 交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
23. (8分)小刚和小明玩抛掷硬币游戏,其规则是:两人轮流同时抛掷三枚均匀的硬币,如果掷得“两正一反”,那么小刚得6分,否则小明得4分.
(1)试用列举法(列表法或画树状图)分析并求出同时抛掷三枚均匀的硬币出现“两正一反”的概率;
(2)按照现在的游戏得分规则,你认为该游戏对两人是否公平?请说明理由:如果不公平,请你设计一种得分方式,使这个游戏对两人都公平,并说明理由
21.(10分)如图已知一次函数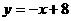 和反比例函数
和反比例函数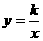
图象在第一象限内有两个不同的公共点A、B.
(1)求实数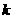 的取值范围;
的取值范围;
(2)若ΔAOB的面积S=24,求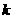 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com