4. 有一种螃蟹，从海上捕获后不放养最多只能存活两天，如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去。假设放养期内蟹的个体重量基本保持不变。现有一经销商，按市场价收购了这种活蟹1000千克放养在塘内，此时的市场价为每千克30元。据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需各种费用支出400元，且平均每天还有10千克蟹死去，假定死蟹均于当天全部售出，售价都是每千克20元。

(1)设x天后每千克活蟹的市场价为P元，写出P关于x的函数关系式；

(2)如果放养x天后将活蟹一次性出售，并记1000千克蟹的销售总额为Q元，写出Q与x的函数关系式；

(3)该经销商将这批蟹放养多少天后出售，可获最大利润(利润＝销售总额－收购成本－费用)？增大利润是多少？

3. 心理学家研究发现，一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力初步增强，中间有一段时间学生的注意力保持较为理想的状态，随后学生的注意力开始分散，经过实验分析可知，学生的注意力y随时间t的变化规律有如下关系(04黄冈)

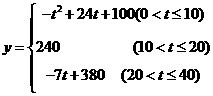
(1)讲课开始后第5分钟与讲课开始第25分钟比较，何时学生的注意力更集中？

(2)讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？

(3)一道数学题，需要讲解24分钟，为了效果较好，要求学生的注意力达到180，那么经过适当安排，老师能否在注意力达到所需的状态下讲解完这道题目？

2.某宾馆有50个房间供游客居住。当每个房间定价为每天180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲。如果游客居住房间，宾馆每天对每个房间需支出20元的各种费用。房价为多少时，宾馆利润最大？

1．　 某新建商场设有百货部、服装部和家电部三个经营部，共有190名售货

员，计划全商场日营业额(指每天卖出商品所收到的总金额)为60万元，由于营业性质不同，分配到三个部的售货员的人数也就不等，根据经验，各类商品每1万元营业额所需售货员人数如表(1)，每1万元营业额所得利润情况如表(2)。商场将计划日营业额分配给三个经营部，设分配给百货部，服装部和家电部的营业额分别为x，y和z(单位：万元，x、y、z都是整数)。(1)请用含x的代数式分别表示y和z；(2)若商场预计每日的总利润为C(万元)，且C满足19≤C≤19.7。问商场应如何分配营业额给三个经营部？各应分别安排多少名售货员？

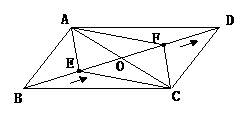
28. (10分)如图：□ABCD的对角线AC、BD相交于点O，BD=12cm，AC=6cm，点E在线段BO上从点B以1cm/s的速度运动，点F在线段OD上从点O以2cm/s的速度运动.

(1)若点E、F同时运动，设运动时间为t秒，当t为何值时，四边形AECF是平行四边形.

(2)在(1)的条件下，①当AB为何值时，四边形AECF是菱形；②四边形AECF可以是矩形吗？为什么？

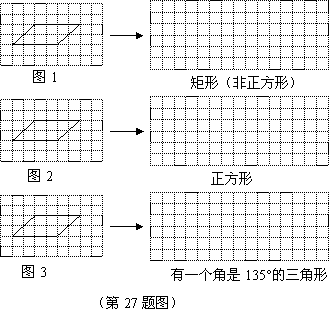
27. (07哈尔滨)现将三张形状、大小完全相同的平行四边形透明纸片，分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合(如图1、图2、图3)．

分别在图1、图2、图3中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，并把这两部分重新拼成符合下列要求的几何图形．

要求：

(1)在左边的平行四边形纸片中画一条裁剪线，然后在右边相对应的方格纸中，按实际大小画出所拼成的符合要求的几何图形；

(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙；

(3)所画出的几何图形的各顶点必须与小正方形的顶点重合．

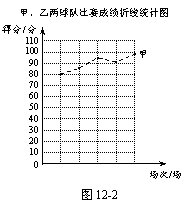
26.甲、乙两支篮球队在集训期内进行了五场比赛，将比赛成绩进行统计后，绘制成如图12-1、图12-2的统计图．

(1)在图12-2中画出折线表示乙队在集训期内这五场比赛成绩的变化情况；

(2)已知甲队五场比赛成绩的平均分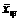=90分，请你计算乙队五场比赛成绩的平均分；

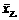(3)就这五场比赛，分别计算两队成绩的极差；

(4)如果从甲、乙两队中选派一支球队参加篮球锦标赛，根据上述统计情况，试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析，你认为选派哪支球队参赛更能取得好成绩？

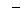
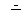
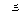
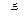
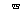
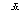
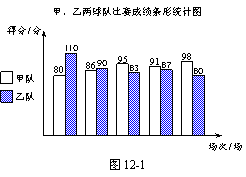
25. 如图， 图是由边长为1的小菱形组成的网格，点A、B在网络格的格点上

(1)请你设计一种规则，用数字或符号表示点A的位置(画图并说明)

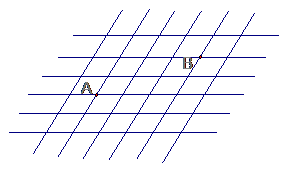(2)以同样的规则表示点B的位置。

24.在等腰三角形ABC中，点D是直线BC上一点，DE∥AC交直线AB于E点， DF∥AB交直线AC于F点，请解答下列问题：

(1)如图，当点D在线段BC上时，证明：DE+DF＝AB

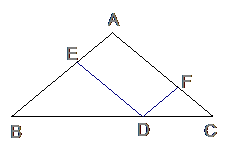(2)当点D在线段BC的延长线上时，请你参考(1)画出正确的图形，并写出线段DE，DF，AB之间的关系(不要证明)

23. 用直尺和圆规作一个菱形，使它的两条对角线分别等于已知线段a、b.

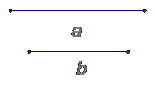如果a、b的长分别为6cm和8cm，请求出此菱形的面积.