14．如图，有一座抛物线型拱桥，在正常水位时水面AB的宽是20米，如果水位上升3米时，水面CD的宽为10米，

　(1)建立如图所示的直角坐标系，求此抛物线的解析式；

　(2)现有一辆载有救援物质的货车从甲地出发，要经过此桥开往乙地，已知甲地到此桥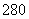千米，(桥长忽略不计)货车以每小时40千米的速度开往乙地，当行驶到1小时时，忽然接到紧急通知，前方连降大雨，造成水位以每小时米的速度持续上涨，(货车接到通知时水位在CD处)，当水位达到桥拱最高点O时，禁止车辆通行；试问：汽车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过多少千米？

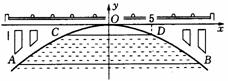
13.某公园要建造一个圆形的喷水池，在水池中央垂直于水面竖一根柱子，上面的A处安装一个喷头向外喷水．连喷头在内，柱高为0.8 m．水流在各个方向上沿形状相同的抛物线路径落下，根据设计图纸已知：图中所示直角坐标系中，水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是

　　　　　　　　　　　　　 ．喷出的水流距水平面的最大高度是多少？如果不计其他因素，那么水池的半径至少为多少时，才能使喷出的水

流都落在水池内？

12．某公司生产的A种产品，它的成本是2元，售价为3元，年销售量为100万件，为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是x(十万元)时，产品的年销售量将是原销售量的y倍，且y＝－x²+x+1，如果把利润看成是销售总额减去成本费和广告费。

　　 (1)试写出年利润S(十万元)与广告费x(十万元)的函数关系式．

(2)如果投入广告费为10-30万元，问广告费在什么范围内，公司获得的年利润随广告费的增大而增次?

(3)在(2)中，投入的广告费为多少万元时，公司获得的年利润最大?是多少?

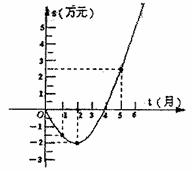
11.某公司推出了一种高效环保洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息，解答下列问题：

(1)由已知图象上的三点坐标，求累积利润s(万元)与时间t(月)之间的函数关系式；

(2)求截止到几月末公司累积利润可达到30万元；

(3)求第8个月公司所获利润是多少万元？

10.在某服装批发市场,某种品牌的时装当季节即将来临时,价格呈上升趋势.设这种时装开始时定价为20元,并且每周(7天)涨价2元,从第6周开始保持30元的价格平稳销售:从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售. (1)试建立销售价Y与周次X之间的函数关系式 (2)若这种时装每件进价Z与周次X之间的关系式为Z=-0.125 (X-8)² +12(1≦x≦16),且为整数,试问：该服装第几周出售时,单件利润最大?最大利润是多少?

9. 某商业公司为指导某种应季商品的生产和销售，对三月份至七月份该商品的售价和成本进行了调研，结果如下：每件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图1)，每件商品的成本Q(元)与时间t(月)的关系可用一条抛物线的一部分上的点来表示(如图2)。

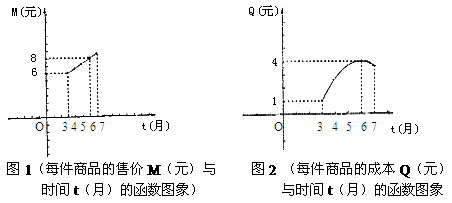
(说明：图1、图2中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本。)

请你根据图象提供的信息回答：

　　 (1)每件商品在3月份出售时的利润(利润＝售价－成本)是多少元？

　　 (2)求图2中表示的每件商品的成本Q(元)与时间t(月)之间的函数关系式(不要求写自变量的取值范围)；

　　 (3)你能求出三月份至七月份每件商品的利润W(元)与时间t(月)之间的函数关系式吗？(请写出计算过程，不要求写自变量的取值范围)若该公司共有此种商品30000件，准备在一个月内全部售完，请你计算一下至少可获利多少元？

8.　 某高科技发展公司投资500万元，成功研制出一种市场需求量较大的高科技替代产品，并投资1500万元进行批量生产。已知生产每件产品的成本为40元。在销售过程中发现：当销售单价定为100元时，年销售量为20万件；销售单价每增加10元，年销售量将减少1万件。设销售单价为x(元)，年销售量为y(万件)，年获利(年获利=年销售额-生产成本-投资)为z(万元)。

(1)试写出y与x之间的函数关系式(不必写出x的取值范围)；

(2)试写出z与x之间的函数关系式(不必写出x的取值范围)；

(3)计算销售单价为160元时的年获利；并说明对同样的年获利，销售单价还可以是多少元，相应的年销售量分别是多少万件；

(4)公司计划：在第一年按年获利最大确定的销售单价，进行销售；第二年年获利不低于1130万元，请你借助函数的大致图像说明，第二年的销售单价x(元)，应确定在什么范围。

7.你知道吗？平时我们在跳大绳时，绳甩到最高处的形状可近似的看为抛物线，如图所示，正在甩绳的甲、乙两名学生拿绳的手间距为4米，距地面均为1米，学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处，绳子甩到最高处时，刚好通过他们的头顶，已知学生丙的身高是1.5米，请你算一算学生丁的身高。

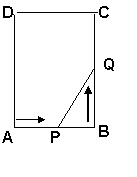
6. 1在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A出发，沿AB边向点B以1cm/秒的速度移动，同时，点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B、C两点后就停止移动，回答下列问题：

(1)运动开始后第几秒时，△PBQ的面积等于8cm2

(2)设运动开始后第t秒时，五边形APQCD的面积为Scm2，写出S与t的函数关系式，并指出自变量t的取值范围；t为何值时S最小？求出S的最小值。

5.如图，等腰Rt△ABC的直角边AB＝2，点P、Q分别从A、C两点同时出发，以相等的速度作直线运动，已知点P沿射线AB运动，点Q沿边BC的延长线运动，PQ与直线相交于点D。

(1)设 AP的长为x，△PCQ的面积为S，求出S关于x的函数关系式；

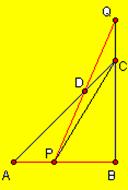(2)当AP的长为何值时，S△PCQ= S△ABC