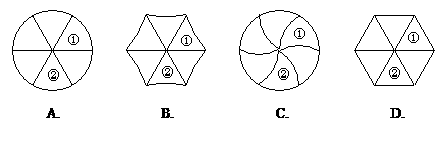
3．下列各图中，既可经过平移，又可经过旋转，由图形①得到图形②的是(　　 ).

2．用反证法证明“若a⊥c,b⊥c,则a∥b”，第一步应假设(　　)

　A．a∥b　 B．a与b垂直　C．a与b不一定平行　D．a与b相交

1．若ax²-5x+3=0是一元二次方程，则不等式3a+6>0的解集是(　 )

　　 A．a>-2　　 B．a<-2　　 C．a>-2且a≠0　　 D．a> 　

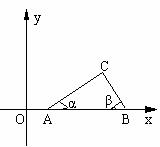
28、(10分)如图，点A(tanα，0)，B(tanβ，0)在x轴的正半轴上，点A在点B的左边，α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角；

　　 (1)若二次函数y=－x²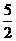－kx+(2+2k－k²)的图象经过A、B两点，求它的解析式。

　　 (2)点C在(1)中求出的二次函数的图象上吗?请说明理由。

27、(10分) 已知Rt△ABC的斜边AB的长为10cm , sinA、sinB是方程

m(x²－2x)+5(x²+x)+12=0的两根。(1)求m的值；(2)求Rt△ABC的内切圆的面积。

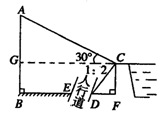
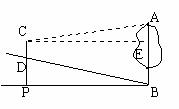
26、(10分)城市规划期间，欲拆除一电线杆AB，已知距电线杆AB水平距离14m的D处有一大坝，背水坡CD的坡度i=2：1，坝高CF为2m，在坝顶C处测得杆顶A的仰角为30°，D、E之间是宽为2m的人行道．试问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封上？请说明理由(在地面上，以点B为圆心，以AB长为半径的圆形区域为危险区域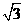．)(≈1.732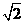，≈1.414)

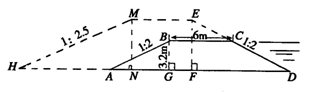
25、(8分)如图，拦水坝的横断面为梯形ABCD，坝顶宽BC为6m，坝高为3.2m，为了提高水坝的拦水能力，需要将水坝加高2m，并且保持坝顶宽度不变，迎水坡CD的坡度不变，但是背水坡的坡度由原来的i=1：2变成i′=1：2.5，(有关数据在图上已注明)．求加高后的坝底HD的长为多少？

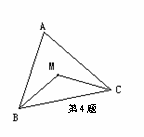
24、 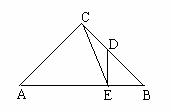(8分)如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连结CE,求sin∠ACE的值.

23、(8分)某商场门前的台阶截面如图所示．已知每级台阶的宽度(如CD)均为30cm，高度(如BE)均为20cm．为了方便残疾人行走，商场决定将其中一个门的门前台阶改造成供轮椅行走的斜坡，并且设计斜坡的倾斜角为9°．请计算从斜坡起点A到台阶前的点B的水平距离．(参考数据：sin9°≈0.16，cos9°≈0.99，tan9°≈0.16)

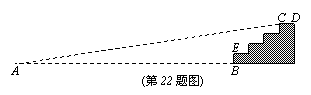
22、 (8分)如图山脚下有一棵树AB，小强从点B沿山坡向上走50m到达点D，用高为1.5m的测角仪CD测得树顶的仰角为10°,已知山坡的坡角为15°,求树AB的高.(精确到0.1m,已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)