4．直接写出答案

(1)(－2)+(+1)＝　 ，(2)5－(－3)＝　 　，

(3)0―(―12)=　　　 　， (4)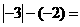　　　　　

3．比较大小：(1)－2 　　　+6 ；(2) 0 　　　　－1.8 ；(3)_____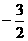

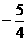
2．的倒数是　　，的相反数是　　，的绝对值是　　，

已知|a|＝3，那么a＝　　　 。

1．盐城市某天中午的温度是5℃，下午由于冷空气南下，到夜间又下降了9℃，则这天夜间的温度是　　　　　 ℃。

20. (本小题满分12 分)有一座抛物线形拱桥，桥下面在正常水位时AB宽20米，水位上升3米就达到警戒线CD，这时水面宽度为10米;

(1)在如图的坐标系中，求抛物线的表达式.

(2)若洪水到来时，再持续多少小时才能到拱桥顶？(水位以每小时0.2米的速度上升)

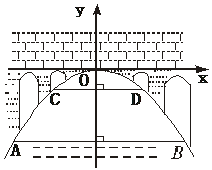
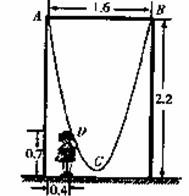
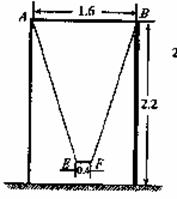
21(本小题满分12 分)如图，一单杠高2.2米，两立柱之间的距离为1.6米，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状．

??(1)一身高0.7米的小孩站在离立柱0.4米处，其头部刚好触上绳子，求绳子最低点到地面的距离；

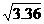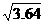??(2)为供孩子们打秋千，把绳子剪断后，中间系一块长为0.4米的木板，除掉系木板用去的绳子后，两边的绳长正好各为2米，木板与地面平行．求这时木板到地面的距离(供选用数据：≈1.8，≈1.9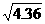，≈2.1．)

19.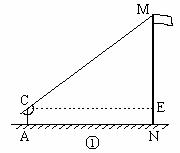 (本小题满分12 分)在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下方案(如图①所示)：

(1)在测点A处安置测倾器，测得旗杆顶部 M 的仰角∠MCE =α；

(2)量出测点A到旗杆底部N的水平距离AN = m；

(3)量出测倾器的高度AC = h．

根据上述测量数据，即可求出旗杆的高度MN．

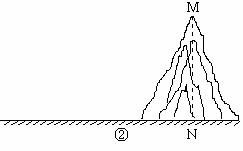
如果测量工具不变，请仿照上述过程，设计一个测量某小山高度(如图②)的方案：

(1)在图②中，画出你测量小山高度 MN 的示意图(标上适当字母)；

(2)写出你设计的方案．

18.(本题满分10分)如图，一位篮球运动员跳起投篮，球沿抛物线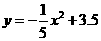运行，然后准确落入篮框内．已知篮框的中心离地面的距离为3.05米．

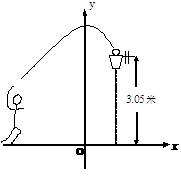(1)球在空中运行的最大高度为多少米？

(2)如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮框中心的水平距离是多少？

16. 在边长为6 cm的正方形中间剪去一个边长为x cm(x<6)的小正方形，剩下的四方框形的面积为y，y与x之间的函数关系是______　　　　　　

三 解答题(共8小题，计52分，解答应写出过程)

17(本题满分6分)求值：sin²45°- cos60°+ tan60°·cos²30°

15. 写出一个开口向上，顶点是y轴上的二次函数的表达式：　　　　　　　　

14. 若函数y=(k²－4)x²+(k+2)x+3是二次函数，则k______