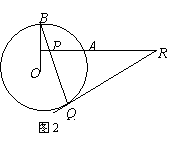
1．如图2，若OA向上平移，变化一中的结论还成立吗？(只需交待判断)

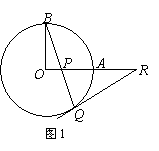
30、有这样一道习题：如图1，已知OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，过Q点作⊙O的切线交OA的延长线于R.说明：RP＝RQ.

请探究下列变化：

变化一：交换题设与结论.

已知：如图1，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点(不与O、A重合)，BP的延长线交⊙O于Q，R是OA的延长线上一点，且RP＝RQ.

求证：RQ为⊙O的切线.

变化二：运动探究：

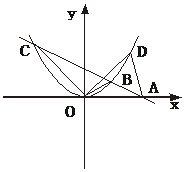
29．如图，直线AB过x轴上的点A(2，0)，且与抛物线y=ax²相交于B、C两点，B点坐标为(1，1).

(1)求直线和抛物线所表示的函数表达式;

(2)在抛物线上是否存在一点D，使得S_△OAD=S_△OBC，若不存在，说明理由；若存在，请求出点D的坐标。

28、2000年度东风公司神鹰汽车改装厂开发出A型农用车，其成本价为每辆2万元，出厂价为每辆2.4万元,年销售价为10000辆,2001年为了支援西部大开发的生态农业建设,该厂抓住机遇,发展企业,全面提高A型农用车的科技含量,每辆农用车的成本价增长率为x，出厂价增长率为0.75x，预测年销售增长率为0.6x.(年利润=(出厂价－成本价)×年销售量)

(1)求2001年度该厂销售A型农用车的年利润y(万元)与x之间的函数关系。

(2)该厂要是2001年度销售A型农用车的年利润达到4028万元，该年度A型农用车的年销售量应该是多少辆？

27．(本小题满分10分)已知某山区的平均气温与该山的海拔高度的关系见下表：

(1)若海拔高度用x(米)表示，平均气温用y(℃)表示，试写出y与x之间的函数关系式；

　　 (2)若某种植物适宜生长在18℃-20℃(包含18℃，也包含20℃)山区，请问该植物适宜种植在海拔为多少米的山区?

26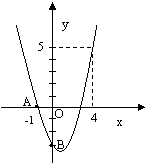． 15．如图二次函数y=ax²+bx+c的图象经过A 、B、C

三点，

(1)观察图象，写出A 、B、C三点的坐标，

并求出抛物线解析式，

(2)求此抛物线的顶点坐标和对称轴

(3)观察图象，当x取何值时，y<0？y=0？y>0?

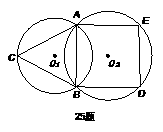
25.如图，⊙O₁和⊙O₂相交于点A、B，AB的长为6cm，在⊙O₁中有一以AB为一边的内接正三角形ABC，在⊙O₂中有一以AB为一边的内接正方形ABDE，求两圆的圆心距O₁O₂的长.

24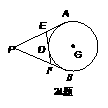．如图，PA、PB、EF都为⊙O的切线，A、B、D为切点，若⊙O的半径为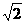，PA=，求：(1)△PEF的周长；(2)∠P的度数.

23．(本题满分6分)

为了从甲、乙两名学生中选拔一人参加全国数学竞赛，李老师每个月对他们的竞赛成绩进行一次测验，下图是两人赛前5次测验成绩的折线统计图．

①分别求出甲、乙两名学生5次测验成绩的平均数、极差及方差并且填在下表中；

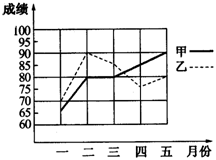②请你参谋一下，李老师应选派哪一名学生参加这次竞赛．请结合所学习的统计知识说明理由．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

解:(1) 填表如下:

(2) 李老师应选派　　　　 参加这次竞赛．

理由：

22．(本题满分6分)

已知：△ABC(如图),

(1)求作：作△ABC的内切圆⊙I.(要求：用尺规作图，保留作图痕迹，不写作法，不要求证明)．

(2) 在题(1)已经作好的图中，若∠BAC=88°，求∠BIC的度数.