2.由圆外一点作圆的切线长为6，过这点作过圆心的割线长为12，则此圆半径长为(　　 )

　　 (A)　 19cm　 (B) 6cm　 (C)　 4.5cm　 (D)以上答案都不对

1.⊙O中直径CD⊥弦AB于E，AB＝6，DE∶CE＝1∶3，则DE的长为(　　 )

　　 (A)　 3　　 (B)　 　　(C)　 2　　　(D)　 6

7.PA、PB分别是⊙O的切线，切点分别为A、B，∠AOB＝144°，则∠P＝　　　　

考点训练：

6.Rt△ABC中两条直角边分别为6cm，8cm，则外接圆半径为　　　　 ,内切圆半径为　　　　

5.从圆外一点P向圆引两条割线PAB、PCD，分别与圆相交于A、B、C、D，如果PA＝4，PC＝3，CD＝5，那么AB＝　　　　

4.圆内两条弦AB与CD相交于E，如果AE＝BE，CE＝9，DE＝4，那么AB＝　　　　

3.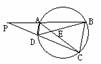如图，圆内接四边形ABCD的BA、CD的延长线交于P，AC、BD交

于E，则图中相似三角形有(　　 )　　　　　　　　

　 (A)2对 (B)3对 (C)4对 (D)5对　　　

2.自圆外一点所作过圆心的割线长是12cm，圆的半径为4cm，则过此点所引的切线长为(　　 )

(A)　　 16cm　 (B)4cm　 (C)4cm　 (D)以上答案都不对

1.圆内两弦相交，其中一条弦长为8cm，且被交点平分，另一条被交点分为1:4两部分，则这条弦长为(　　 )

　 (A)2cm　　 (B)8cm　　 (C)10cm　　 (D)16cm　

4．　 注意(1)相交弦定理、切割线定理及其推论统称为圆幂定理，圆幂定理是圆和相似

三角形结合的产物。这几个定理可统一记忆成一个定理：过圆内或圆外一点作圆的两条割线，则这两条割线被圆截出的两弦被定点分(内分或外分)成两线段长的积相等(至于切线可看作是两条交点重合的割线)。使用时注意每条线段的两个端点一个是公共点，另一个是与圆的交点；

(2)见圆中有两条相交想到相交弦定理；见到切线与一条割线相交则想到切割线定理；若有两条切线相交则想到切线长定理，并熟悉此时图形中存在着一个以交点和圆心连线为对称轴的对称图形。

[考查重点与常见题型]

证明等积式、等比式及混合等式等。此种结论的证明重点考查了相似三角形，切割线定

理及其推论，相交弦定理及圆的一些知识。常见题型以中档解答题为主，也有一些出现在选择题或填空题中。

[预习练习]