
题目列表(包括答案和解析)
24. 在平面直角坐标系
在平面直角坐标系 中,抛物线
中,抛物线 与
与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,点
,点 的坐标为
的坐标为 ,将直线
,将直线 沿
沿 轴向上平移3个单位长度后恰好经过
轴向上平移3个单位长度后恰好经过 两点.
两点.
(1)求直线 及抛物线的解析式;
及抛物线的解析式;
(2)设抛物线的顶点为 ,点
,点 在抛物线的对称轴上,且
在抛物线的对称轴上,且 ,求点
,求点 的坐标;
的坐标;
(3)连结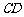 ,求
,求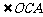 与
与 两角和的度数.
两角和的度数.
[解析]
⑴  沿
沿 轴向上平移3个单位长度后经过
轴向上平移3个单位长度后经过 轴上的点
轴上的点 ,
,
 .
.
设直线 的解析式为
的解析式为 .
.
 在直线
在直线 上,
上,
 .
.
解得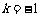 .
.
 直线
直线 的解析式为
的解析式为 .···························································· 1分
.···························································· 1分
 抛物线
抛物线 过点
过点 ,
,

解得
 抛物线的解析式为
抛物线的解析式为 .························································· 2分
.························································· 2分
 ⑵ 由
⑵ 由 .
.
可得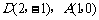 .
.
 ,
, ,
, ,
, .
.
可得 是等腰直角三角形.
是等腰直角三角形.
 ,
,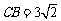 .
.
如图1,设抛物线对称轴与 轴交于点
轴交于点 ,
,
 .
.
过点 作
作 于点
于点 .
.
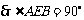 .
.
可得 ,
, .
.
在 与
与 中,
中, ,
, ,
,
 .
.
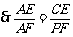 ,
, .
.
解得 .
.
 点
点 在抛物线的对称轴上,
在抛物线的对称轴上,
 点
点 的坐标为
的坐标为 或
或 .······························································· 5分
.······························································· 5分
⑶ 解法一:
 如图2,作点
如图2,作点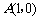 关于
关于 轴的对称点
轴的对称点 ,则
,则 .
.
连结 ,
,
可得 ,
, .
.
由勾股定理可得 ,
, .
.
又 ,
,
 .
.
 是等腰直角三角形,
是等腰直角三角形, ,
,
 .
.
 .
.
 .
.
即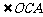 与
与 两角和的度数为
两角和的度数为 .··················································· 7分
.··················································· 7分
 解法二:
解法二:
如图3,连结 .
.
同解法一可得 ,
,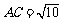 .
.
在 中,
中, ,
, ,
,
 .
.
在 和
和 中,
中,
 ,
,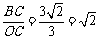 ,
, .
.
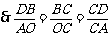 .
.
 .
.
 .
.
 ,
,
 .
.
即 与
与 两角和的度数为
两角和的度数为 .··················································· 7分
.··················································· 7分
[点评]
本题设计得很精致,将几何与函数完美的结合在一起,对学生综合运用知识的能力要求较高,本题3问之间层层递进,后两问集中研究角度问题。中等层次的学生能够做出第⑴问,中上层次的学生可能会作出第⑵问,但第⑵问中符合条件的 点有两个,此时学生易忽视其中某一个,成绩较好的学生才可能作出第⑶问,本题是拉开不同层次学生分数的一道好题。
本题考点:函数图形的平移、一次函数解析式的确定、二次函数解析式的确定、相似三角形、
点有两个,此时学生易忽视其中某一个,成绩较好的学生才可能作出第⑶问,本题是拉开不同层次学生分数的一道好题。
本题考点:函数图形的平移、一次函数解析式的确定、二次函数解析式的确定、相似三角形、
等腰直角三角形的判定及性质、勾股定理
难度系数:第⑴问:5.5;第⑵问:3.5;第⑶问:2.5
23.已知:关于 的一元二次方程
的一元二次方程 .
.
 (1)求证:方程有两个不相等的实数根;
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为 ,
,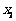 (其中
(其中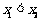 ).若
).若 是关于
是关于 的函数,且
的函数,且 ,求这个函数的解析式;
,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图象回答:当自变量 的取值范围满足什么条件时,
的取值范围满足什么条件时, .
.
[解析]
⑴  是关于
是关于 的一元二次方程,
的一元二次方程,
 .
.
 当
当 时,
时, ,即
,即 .
.
 方程有两个不相等的实数根.································································· 2分
方程有两个不相等的实数根.································································· 2分
⑵ 解:由求根公式,得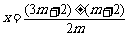 .
.
 或
或 .················································································ 3分
.················································································ 3分
 ,
,
 .
.
 ,
,
 ,
, .·············································································· 4分
.·············································································· 4分

 .
.
即 为所求.··········· 5分
为所求.··········· 5分
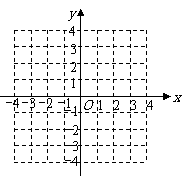
⑶ 在同一平面直角坐标系中分别画出
 与
与 的图象.
的图象.
···················································· 6分
由图象可得,当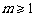 时,
时, . 7分
. 7分
[点评] 本题是一道代数综合题,综合了一元二次方程、一次函数、用函数的观点看不等式等知识。对考生要求较高。 本题考点:一元二次方程根的判别式、代数式的大小比较、一次函数、用函数的观点看不等式。 难度系数:第⑴问:0.65;第⑵问:0.5;第⑶问:0.45
易忽视点:第⑶问中 。
。
22.(本小题满分4分)
已知等边三角形纸片 的边长为
的边长为 ,
, 为
为 边上的点,过点
边上的点,过点 作
作 交
交 于点
于点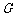 .
. 于点
于点 ,过点
,过点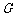 作
作 于点
于点 ,把三角形纸片
,把三角形纸片 分别沿
分别沿 按图1所示方式折叠,点
按图1所示方式折叠,点 分别落在点
分别落在点 ,
, ,
, 处.若点
处.若点 ,
, ,
, 在矩形
在矩形 内或其边上,且互不重合,此时我们称
内或其边上,且互不重合,此时我们称 (即图中阴影部分)为“重叠三角形”.
(即图中阴影部分)为“重叠三角形”.


(1)若把三角形纸片 放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点
放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点 恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形
恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形 的面积;
的面积;
(2)实验探究:设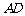 的长为
的长为 ,若重叠三角形
,若重叠三角形 存在.试用含
存在.试用含 的代数式表示重叠三角形
的代数式表示重叠三角形 的面积,并写出
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).

解:(1)重叠三角形 的面积为
;
的面积为
;
(2)用含 的代数式表示重叠三角形
的代数式表示重叠三角形 的面积为
;
的面积为
; 的取值范围为 .
的取值范围为 .
[解析]
⑴ 重叠三角形 的面积为
的面积为 . 1分
. 1分
⑵ 用含 的代数式表示重叠三角形
的代数式表示重叠三角形 的面积为
的面积为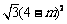 ;··················· 2分
;··················· 2分
 的取值范围为
的取值范围为 .······································································ 4分
.······································································ 4分
[点评] 本题是一个探究性的折叠问题,考核了学生对新知识的探究能力。本题题目较长,理解题意是解决本题的关键。 本题考点:等边三角形的性质、图形的折叠、平行四边形的性质等。 难度系数:0.5
21.(本小题满分5分)列方程或方程组解应用题:
京津城际铁路将于2008年8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米?
[解析]
设这次试车时,由北京到天津的平均速度是每小时 千米,则由天津返回北京的平均速度是每小时
千米,则由天津返回北京的平均速度是每小时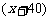 千米. 1分
千米. 1分
依题意,得 .···································································· 3分
.···································································· 3分
解得 .································································································· 4分
.································································································· 4分
答:这次试车时,由北京到天津的平均速度是每小时200千米.····················· 5分
[点评] 本题也是一道与时事紧密相关的数学题,在考核学生数学知识的同时让学生了解时事,本题着重考核了学生应用适当的数学模型解决实际问题的能力。 本题考点:列一元一次方程解应用题 难度系数:0.6 易忽视点:预计时间为30分钟,学生易忽视。
19.(本小题满分5分)
 已知:如图,在
已知:如图,在 中,
中, ,点
,点 在
在 上,以
上,以 为圆心,
为圆心, 长为半径的圆与
长为半径的圆与 分别交于点
分别交于点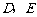 ,且
,且 .
.
(1)判断直线 与
与 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若 ,
, ,求
,求 的长.
的长.
[解析]
⑴ 直线 与
与 相切. 1分
相切. 1分
 证明:如图1,连结
证明:如图1,连结 .
.
 ,
,
 .
.
 ,
,  .
.
又 ,
,
 .
.
 .
.
 直线
直线 与
与 相切.············································································· 2分
相切.············································································· 2分
⑵ 解法一:如图1,连结 .
.
 是
是 的直径,
的直径,  .
.
 ,
,
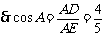 .···················································································· 3分
.···················································································· 3分
 ,
, ,
,
 .············································································ 4分
.············································································ 4分
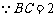 ,
,  .·································································· 5分
.·································································· 5分
解法二:如图2,过点 作
作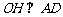 于点
于点 .
.  .
.

 ,
,
 .······· 3分
.······· 3分
 ,
, ,
,
 .························ 4分
.························ 4分
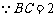 ,
,
 .······························································································· 5分
.······························································································· 5分
[点评] 本题是一道与圆相关的综合题,第⑴问是常规的切线证明,第⑵问则是可以综合相似、三角函数、勾股定理等知识解决,是考核学生综合能力的一道好题。 本题考点:圆切线的判定、圆的有关性质(垂径定理、直径所对的圆周角是直角)、相似(或三角函数、勾股定理) 难度系数:第⑴问:0.6;第⑵问:0.5
18.(本小题满分5分)
如图,在梯形 中,
中, ,
, ,
,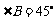 ,
, ,
, ,求
,求 的长.
的长.
[解析]
解法一:
如图1,分别过点 作
作 于点
于点 ,
,
 于点
于点 .································ 1分
.································ 1分

 .
.
 又
又 ,
,
 四边形
四边形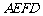 是矩形.
是矩形.
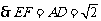 .································· 2分
.································· 2分
 ,
,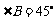 ,
, ,
,
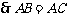 .
.
 .
.
 ,
,
 ························································································· 4分
························································································· 4分
在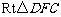 中,
中, ,
,
 .··············································· 5分
.··············································· 5分
解法二:
如图2,过点 作
作 ,分别交
,分别交 于点
于点 .····························· 1分
.····························· 1分
 ,
,

 .
.
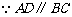 ,
,
 .
.
在 中,
中, ,
,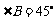 ,
, ,
,
 ···································································· 2分
···································································· 2分
在 中,
中, ,
, ,
, ,
,
 .
.
 .····················································································· 4分
.····················································································· 4分
在 中,
中, ,
,
 .···························································· 5分
.···························································· 5分
[点评] 统观北京及全国各地中考试卷,几何中的计算往往会与两个知识点有关:①圆;②梯形。
本题考点:等腰直角三角形的性质、特殊四边形的性质、勾股定理.
难度系数:0.6.
17.(本小题满分5分)
已知 ,求
,求 的值.
的值.
[解析]

 ····························································································· 2分
····························································································· 2分
 .······································································································ 3分
.······································································································ 3分
当 时,
时, .··············································································· 4分
.··············································································· 4分
原式 .················································································· 5分
.················································································· 5分
[点评] 试卷到本题以后整体难度有所上升。本题考核了分式的化简求值。解决本题的关键是分式的正确化简、将已知条件的适当变形代入消元。 本题考点:分式的化简求值。 难度系数:0.65

16. (本小题满分5分)
(本小题满分5分)
如图,已知直线 经过点
经过点 ,求此直线与
,求此直线与 轴,
轴, 轴的交点坐标.
轴的交点坐标.
[解析]
由图象可知,点 在直线
在直线 上, 1分
上, 1分
 .
.
解得 .·································································································· 2分
.·································································································· 2分
 直线的解析式为
直线的解析式为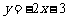 .······································································· 3分
.······································································· 3分
令 ,可得
,可得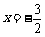 .
.
 直线与
直线与 轴的交点坐标为
轴的交点坐标为 .······························································ 4分
.······························································ 4分
令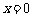 ,可得
,可得 .
.
 直线与
直线与 轴的交点坐标为
轴的交点坐标为 .······························································· 5分
.······························································· 5分
[点评] 本题考核的是一次函数中较为基础的知识.题目难度较小 本题考点:一次函数解析式的确定、一次函数与坐标轴的交点的确定. 难度系数:0.75
15.(本小题满分5分)
已知:如图, 为
为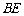 上一点,点
上一点,点 分别在
分别在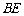 两侧.
两侧.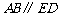 ,
, ,
, .求证:
.求证: .
.
[解析]
 ,
,
 .·································································································· 2分
.·································································································· 2分
在 和
和 中,
中,

 .························································································ 4分
.························································································ 4分
 .·································································································· 5分
.·································································································· 5分
[点评] 本题是一道很简单的全等证明,纵观近几年北京市中考数学试卷,每一年都有一道比较简单的几何证明题:只需证一次全等,无需添加辅助线,且全等的条件都很明显。本题是解答题中几何的第1道题,难度较小是为了让所有的考生在进入解答题后都有一个顺利的开端,避免产生畏惧心理,这样考试才有信心做后面较难的题目。 本题考点:全等三角形的判定(SAS)和性质. 难度系数:0.9
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com