
题目列表(包括答案和解析)
28.(1)解: 函数
函数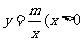 ,
, 是常数)图象经过
是常数)图象经过 ,
, . 1分
. 1分
设 交于点
交于点 ,据题意,可得
,据题意,可得 点的坐标为
点的坐标为 ,
, 点的坐标为
点的坐标为 ,
,
 点的坐标为
点的坐标为 ,······································································ 1分
,······································································ 1分
 ,
,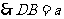 ,
, .
.
由 的面积为4,即
的面积为4,即 ,········································· 1分
,········································· 1分
得 ,
, 点
点 的坐标为
的坐标为 .···················································· 1分
.···················································· 1分
(2)证明:据题意,点 的坐标为
的坐标为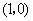 ,
, ,
,
 ,易得
,易得 ,
, ,
,
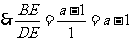 ,
, .·············································· 1分
.·············································· 1分

 .····················································································· 1分
.····················································································· 1分
(3)解: ,
, 当
当 时,有两种情况:
时,有两种情况:
①当 时,四边形
时,四边形 是平行四边形,
是平行四边形,
由(2)得, ,
, ,得
,得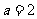 .
.
 点
点 的坐标是(2,2).······························································ 1分
的坐标是(2,2).······························································ 1分
设直线 的函数解析式为
的函数解析式为 ,把点
,把点 的坐标代入,
的坐标代入,
得 解得
解得
 直线
直线 的函数解析式是
的函数解析式是 . 1分
. 1分
②当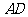 与
与 所在直线不平行时,四边形
所在直线不平行时,四边形 是等腰梯形,
是等腰梯形,
则 ,
, ,
, 点
点 的坐标是(4,1).···························· 1分
的坐标是(4,1).···························· 1分
设直线 的函数解析式为
的函数解析式为 ,把点
,把点 的坐标代入,
的坐标代入,
得 解得
解得
 直线
直线 的函数解析式是
的函数解析式是 . 1分
. 1分
综上所述,所求直线 的函数解析式是
的函数解析式是 或
或 .
.
27.(1)证明: ,
,
 .················································································· 1分
.················································································· 1分
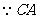 平分
平分 ,
,
 ,··········································································· 1分
,··········································································· 1分
 ,··············································································· 1分
,··············································································· 1分
又 ,
,
 .················································································· 1分
.················································································· 1分
 梯形
梯形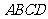 是等腰梯形,即
是等腰梯形,即 .········································· 1分
.········································· 1分
(2)解:如图3,作 ,
, ,
,
垂足分别为 ,则
,则 .
.
 在
在 中,
中, ,
, .…………1分
.…………1分
又 ,且
,且 ,
,
 ,得
,得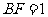 .……………………1分
.……………………1分
同理可知,在 中,
中, .……………1分
.……………1分
 ,
, .
.
又 ,
, ,
,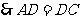 .
.
 ,
, .··························································· 1分
.··························································· 1分
 ,
, ,
, 四边形
四边形 是平行四边形,
是平行四边形,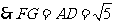 . 1分
. 1分
 .
.
28. 如图,在直角坐标平面内,函数
如图,在直角坐标平面内,函数 (
( ,
, 是常数)的图象经过
是常数)的图象经过 ,
,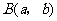 ,其中
,其中 .过点
.过点 作
作 轴垂线,垂足为
轴垂线,垂足为 ,过点
,过点 作
作 轴垂线,垂足为
轴垂线,垂足为 ,连结
,连结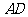 ,
, ,
, .
.
(1)若 的面积为4,求点
的面积为4,求点 的坐标;(4分)
的坐标;(4分)
(2)求证: ;(2分)
;(2分)
(3)当 时,求直线
时,求直线 的函数解析式.(4分)
的函数解析式.(4分)
26.(本小题满分8分)
已知四边形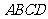 中,
中, ,
, ,
, ,
, ,
, ,
, 绕
绕 点旋转,它的两边分别交
点旋转,它的两边分别交 (或它们的延长线)于
(或它们的延长线)于 .
.
当 绕
绕 点旋转到
点旋转到 时(如图1),易证
时(如图1),易证 .
.
当 绕
绕 点旋转到
点旋转到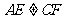 时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段
时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段 ,
, 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.

29、(11分)如图1,矩形纸片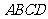 的边长分别为
的边长分别为 .将纸片任意翻折(如图2),折痕为
.将纸片任意翻折(如图2),折痕为 .(
.( 在
在 上),使顶点
上),使顶点 落在四边形
落在四边形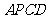 内一点
内一点 ,
, 的延长线交直线
的延长线交直线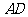 于
于 ,再将纸片的另一部分翻折,使
,再将纸片的另一部分翻折,使 落在直线
落在直线 上一点
上一点 ,且
,且 所在直线与
所在直线与 所在直线重合(如图3)折痕为
所在直线重合(如图3)折痕为 .
.
(1)猜想两折痕 之间的位置关系,并加以证明.
之间的位置关系,并加以证明.
(2)若 的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕
的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕 间的距离有何变化?请说明理由.
间的距离有何变化?请说明理由.
 (3)若
(3)若 的角度在每次翻折的过程中都为
的角度在每次翻折的过程中都为 (如图4),每次翻折后,非重叠部分的四边形
(如图4),每次翻折后,非重叠部分的四边形 ,及四边形
,及四边形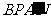 的周长与
的周长与 有何关系,为什么?
有何关系,为什么?
26、(12分)为保证交通安全,汽车驾驶员必须知道汽车刹车后的停止距离(开始刹车到车辆停止车辆行驶的距离)与汽车行驶速度(开始刹车时的速度)的关系,以便及时刹车.
下表是某款车在平坦道路上路况良好时刹车后的停止距离与汽车行驶速度的对应值表:
|
行驶速度(千米/时) |
 |
 |
 |
 |
|
停止距离(米) |
 |
 |
 |
 |
(1)设汽车刹车后的停止距离 (米)是关于汽车行驶速度
(米)是关于汽车行驶速度 (千米/时)的函数,给出以下三个函数:①
(千米/时)的函数,给出以下三个函数:① ;②
;② ;③
;③ ,请选择恰当的函数来描述停止距离
,请选择恰当的函数来描述停止距离 (米)与汽车行驶速度
(米)与汽车行驶速度 (千米/时)的关系,说明选择理由,并求出符合要求的函数的解析式;
(千米/时)的关系,说明选择理由,并求出符合要求的函数的解析式;
(2)根据你所选择的函数解析式,若汽车刹车后的停止距离为 米,求汽车行驶速度.
米,求汽车行驶速度.
26、 如图,一次函数
如图,一次函数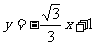 的图象与
的图象与 轴、
轴、 轴分别交于点A、B,以线段AB
轴分别交于点A、B,以线段AB
为边在第一象限内作等边△ABC,
(1) 求△ABC的面积;
(2) 如果在第二象限内有一点P( ),试用含
),试用含 的式
的式
子表示四边形ABPO的面积,并求出当△ABP的 面积与△ABC的面积相等时 的值;
的值;
(3) 在 轴上,存在这样的点M,使△MAB为等腰三角形.
轴上,存在这样的点M,使△MAB为等腰三角形.
请直接写出所有符合要求的点M的坐标.
26、(12分)蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间 (月份)与市场售价
(月份)与市场售价 (元/千克)的关系如下表:
(元/千克)的关系如下表:
上市时间 (月份) (月份) |
1 |
2 |
3 |
4 |
5 |
6 |
市场售价 (元/千克) (元/千克) |
10.5 |
9 |
7.5 |
6 |
4.5 |
3 |
这种蔬菜每千克的种植成本 (元/千克)与上市时间
(元/千克)与上市时间 (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价 (元/千克)关于上市时间
(元/千克)关于上市时间 (月份)的函数关系式;
(月份)的函数关系式;
(2)若图中抛物线过 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;
 (3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)
24、(12分)某工厂生产某种产品按质量分为10个档次,生产第一档次(即最低档次)的产品一天生产76件,每件利润10元,每提高一个档次,利润每件增加2元。
(1)当每件利润为16元时,此产品的质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量就减少4件,若生产第x档次的产品一天的总利润为y元(其中x为正整数且1≤x≤10),求出y关于x的关系式,若生产某档次产品一天的总利润为1080元。该工厂生产的是第几档次的产品?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com