24. 某公司试销一种成本单价为500元/件的新产品，规定试销时的销售单价不低

于成本单价，又不高于800元/件，经试销调查发现销售量y(件)与销售单

价x(元/件)可近似看作一次函数的关系(如图所示)．

(1)根据图象，求一次函数的表达式；

(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元．①试用销

售单价x表示毛利润S；②试问销售单价定为多少时，该公司获得最大毛利润？

最大毛利润是多少？此时的销售量是多少？

26．(1)画出角平分线、线段的垂直平分线。············ 3分(仅画出一条得2分)

(2)①　··························································································· 4分

② 方法一：∵EF是线段CD的垂直平分线，

∴FC=FD ·································································································· 5分

∵△COD为直角三角形，E为CD的中点

∴

∴

设CD与OP相交于点G，

∵

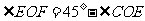
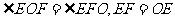∴································································ 6分

又CE=OE=EF，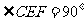

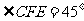∴，同理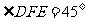

∴，△CDF等腰为直角三角形。·································· 7分

方法二：过点F作FM⊥OA、FN⊥OB，垂足分别为M、N。····· 5分

∵OP是∠AOB的平分线，

∴FM=FN。

又EF是CD的垂直平分线，

∴FC=FD。

∴Rt△CFM≌Rt△DFN，∠CFM=∠DFN。······································ 6分

在四边形MFNO中，由∠AOB=∠FMO=∠FNO=90°，得∠MFN=90°

∴∠CFD=∠CFM+∠MFD=∠DFN+∠MFD=∠MFN=90°

∴△CDF为等腰直角三角形。··························································· 7分

25．(1)格点坐标为：、、、、

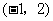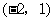、、、·················································· 2分

(2)满足条件的直线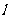共有28条 ·································································· 4分

(3)“直线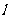同时经过第一、二、四象限”记为事件A，它的发生有4种可能，所有事件A发生的概率P(A)=，即直线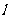同时经过第一、二、四象限的概率为．···················· 6分

24．(1)由题意，得c=3，a+b+3=0，，即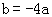　 2分(仅列出一个关系式，得1分)

解方程组，得

∴抛物线所对应的函数关系式为，

抛物线的顶点坐标为·································································· 4分

(2)画图．······································································································ 5分

由图像得，当1<x<3时，y<0。···························································· 6分

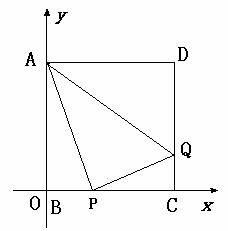
25. 如图所示，在平面直角坐标系中，正方形ABCD的边长为4，点B在系原点上，

P是BC上一动点，QP⊥AP交DC于Q，设PB=x，△ADQ的面积为y.

(1)求y与x之间的函数关系式，并写出自变量x的取值范围.

(2)(1)中函数若是一次函数，求出直线与两坐标轴围成的三角形面积，若是二

次函数，请利用配方法求出抛物线的对称轴和顶点坐标.

(3)点P是否存在这样的位置，使△APB的面积是△ADQ的面积的，若存在，

求出点P的坐标，若不存在，请说明理由.

24. 如图(a)，已知AB是⊙O的直径，CB是⊙O的切线，B为切点，D是⊙O上一点(不A、B重合).

(1)　　 求证：∠DAB =∠DBC；

(2)　　 若AB不是⊙O的直径，其它条件不变，(1)中的结论还成立吗？若成立

则给出你的证明；若不成立，请说明理由.

23．(本题满分为9分)某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不及格”、“及格”、“优秀”三个等级，为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考试考分等级，所绘制的统计图如图所示，试结合图形信息回答下列问题：

(1)　　 这32名学生培训前考分的中位数所在的等级是　　　 ，培训后考分的中位数所在的等级是　　　　 ．

(2)　　 这32名学生经过培训，考分等级

“不合格”的百分比由　　　 下降到　　　　　 ．

(3)估计该校整个初二年级中，培训后考分

等级为“合格”与“优秀”的学生共有　　　　 名．

(4)你认为上述估计合理吗？理由是什么？

答：　　　　　　 　，理由　　　　　　　　　　　　　　 　　　　　　　．

22．(本题为2分+2分+5分)如图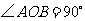，，点C、D分别在OA、OB上。

⑴ 尺规作图(不写作法，保留作图痕迹)：作的平分线OP；作线段CD的垂直平分线EF，分别与CD、OP相交于E、F；连结OE、CF、DF。

⑵ 在所画图中，

① 线段OE与CD之间有怎样的数量关系：_____________。

② 求证：△CDE为等腰直角三角形。

21、(本小题满分8分)

如图，⊙O的半径是，圆心与坐标原点重合，在直角坐标系中，把横坐标、纵坐标都是整数的点称为格点。

⑴　　 　写出⊙O上所有格点的坐标：

___________________________________________________。

⑵ 设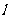为经过⊙O上任意两个格点的直线。

① 满足条件的直线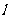共有多少条？

② 求直线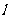同时经过第一、二、四象限的概率。

20．某校七年级在学校团委的组织下，围绕“八荣八耻”开展了一次知识竞赛活动，

竞赛规则：每班代表队都必须回答27道题，答对一题得5分，答错或不答都倒扣1分。　

(1)在比赛到第18题结束时，(3)班代表队得分为78分，这时(3)班答对了多少道题？(7分)

(2)比赛规定，只有得分超过100分(含100分)时才能获奖。在第(1)小题的条件下，(3)班代表队在后面的比赛中至少还要答对多少题才有可能获奖？请简要说明理由。