
题目列表(包括答案和解析)
5. 相关综合题
例47(天津市2007)已知抛物线y=x2+bx+c与x轴只有一个交点,且交点为A(2,0).
(I)求b、c的值;
(II)若抛物线与y轴的交点为B,坐标原点为O,求△OAB的周长(答案可带根号)
例48(重庆市2007年)已知一次函数 y = ax + c 与二次函数 y = ax2 + bx + c,它们在同一坐标系内的大致图象是( ).

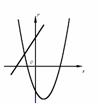
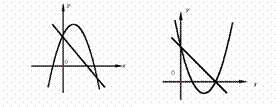 (A) (B) (C)
(D)
(A) (B) (C)
(D)
例49 抛物线 y = x2 - 2x + c 与 x 轴交于A、B两点(点A在点B的左侧),与 y 轴交于点C,且OC =OB,求此抛物线的函数解析式及三角形ABC的面积.
 例50 ★★(吉林省2007)如图、已知抛物线y=x2 –ax+a+2与x轴交于A、B两点,与y轴交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C。动点P以每秒2个单位长度的速度从点C出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从A出发,沿A→B运动。连结PQ、CB.设点P的运动时间为t秒
.
例50 ★★(吉林省2007)如图、已知抛物线y=x2 –ax+a+2与x轴交于A、B两点,与y轴交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C。动点P以每秒2个单位长度的速度从点C出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从A出发,沿A→B运动。连结PQ、CB.设点P的运动时间为t秒
.
(1)求a的值;
(2)当t为何值时,PQ平行于y轴?
(3)当四边形PQBC的面积等于14时,
求t的值
例51 (吉林省2007) 下列图中阴影部分的面积与算式| |+(
|+( )2
+ 2-1的结果相同的是 ( )
)2
+ 2-1的结果相同的是 ( )


例52 ★★(海口市课改实验区2007)已知抛物线y = x2 + (2n–1)x + n2–1(n为常数)
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上位于x轴的下方,且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线与另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由。
4. 二次函数的应用
 例45 (吉林省2007)如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距. 某项研究表明,一般情况下人的身高h是指距d的一次函数. 下表是测得的指距与身高的一组数据:
例45 (吉林省2007)如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距. 某项研究表明,一般情况下人的身高h是指距d的一次函数. 下表是测得的指距与身高的一组数据:
|
指距d(cm) |
20 |
21 |
22 |
23 |
|
身高h(cm) |
160 |
169 |
178 |
187 |
(1) 求出h与d之间的函数关系式(不要求写出自变量d的取值范围):
(2) 某人身高为196cm,一般情况下他的指距应是多少?
 例46★★(山西省2007)若用(1)、(2)、(3)、(4)四幅图像分别表示量之间的关系,请按图像所给顺序,将下面的a、b、c、d对应排序
例46★★(山西省2007)若用(1)、(2)、(3)、(4)四幅图像分别表示量之间的关系,请按图像所给顺序,将下面的a、b、c、d对应排序
(a) 小车从光滑的斜面上滑下(小车速度与时间的关系)
(b) 一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物重量的关系)
(c) 运动员推出去的铅球(铅球高度与时间的关系)
(d) 小杨从A到B后,停留一段时间,然后按原速度返回(路程与时间的关系)
正确的顺序是:( )
(A)(c)(d)(b)(a) (B)(a)(b)(c)(d)
(C)(b)(c)(a)(d) (D)(d)(a)(c)(b)
4、 如图,矩形ABCD,AB = 3,AD = 4,以AD为直径作半圆, 为BC上一动点,可与B,C重合,
为BC上一动点,可与B,C重合, 交半圆于
交半圆于 ,设
,设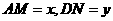 ,求出
,求出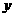 关于自变量
关于自变量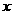 的函数关系式,并求出自变量
的函数关系式,并求出自变量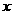 的取值范围.
的取值范围.
3、如图,Rt△ABO的顶点A是双曲线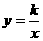 与直线
与直线 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥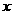 轴于B且S△ABO=
轴于B且S△ABO=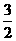
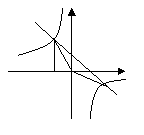 (1)求这两个函数的解析式
(1)求这两个函数的解析式
(2)求直线与双曲线的两个交点A,C的坐标和
△AOC的面积。
2、已知一次函数 和反比例函数
和反比例函数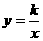 (
(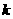 ≠0)
≠0)
(1)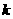 满足什么条件时这两个函数在同一坐标系xoy中图象有两个公共交点。
满足什么条件时这两个函数在同一坐标系xoy中图象有两个公共交点。
(2)设(1)中的两个公共点为A,B,则∠AOB是锐角还是钝角。
1、已知 与
与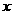 成反比例,
成反比例, 与
与 成正比例,并且当
成正比例,并且当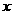 =3时,
=3时,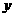 =5,当
=5,当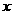 =1时,
=1时,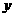 =-1;求
=-1;求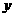 与
与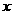 之间的函数关系式.
之间的函数关系式.
4、反比例函数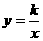 与一次函数
与一次函数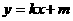 的图象有一个交点是(-2,1),则它们的另一个交点的坐标是
.
的图象有一个交点是(-2,1),则它们的另一个交点的坐标是
.
3、 如图,面积为3的矩形OABC的一个顶点B在反比例函数
如图,面积为3的矩形OABC的一个顶点B在反比例函数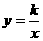 的图象上,另三点在坐标轴上,则
的图象上,另三点在坐标轴上,则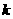 =
.
=
.
2、已知函数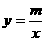 ,当
,当 时,
时,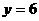 ,则函数的解析式是
;
,则函数的解析式是
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com